Difference between revisions of "Finite State Machines"
(→Mealy Machines) |
(→Mealy Machines) |
||
| Line 53: | Line 53: | ||
'''Each transition is labeled: ''Input / Output'' ''' | '''Each transition is labeled: ''Input / Output'' ''' | ||
| − | This can be represented in the following State Transition | + | This can be represented in the following State Transition Table: |
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Original State !! Input!! New State !! Output | ||
| + | |- | ||
| + | | Example || Example || Example || Example | ||
| + | |- | ||
| + | | Example || Example || Example || Example | ||
| + | |- | ||
| + | | Example || Example || Example || Example | ||
| + | |} | ||
Revision as of 07:32, 22 May 2017
Contents
[hide]Definition
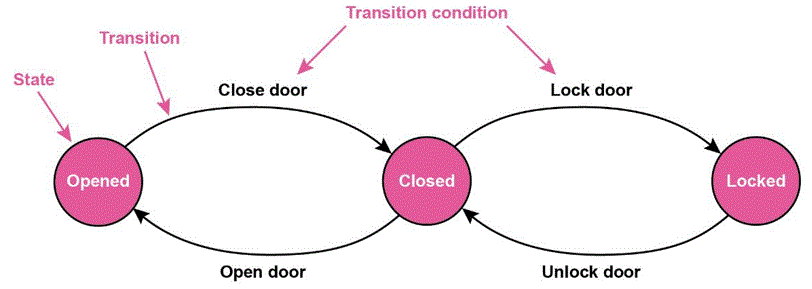
A finite state machine is a way of breaking down a problem into several mutually independent states that are only able to change when a transition occurs. A transition occurs when an input is given. The machine can only be in one state at a time. The state the machine is in at any time is referred to as the '"current state'". Any change to the state is known as a "'transition'".
A finite state machine is not a physical machine. It is an abstract representation of an algorithm, showing how something changes in response to inputs or events. It is used to design computer programs and some logic circuits.The machine also enables it to check if the input is valid. This means that it has a wide variety of practical uses. One of these is a vending machine, which requires a valid input to determine what product is dispensed. Any input that is invalid will simply be rejected.
Where are they used:
- Robotics
- Video games industry
- Design of digital hardware systems
- Design of compilers and network protocols
- Definition of languages, and to decide whether a particular word is allowed in a language
Finite State Automaton
A finite state automaton is a finite state machine which has no output. It has a start state and a set of end/accept states. If the automaton can reach an end state then the input is accepted.
Representing Finite State Machines
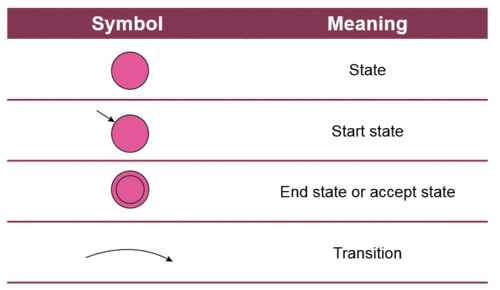
Finite state machines can be represented as diagrams.
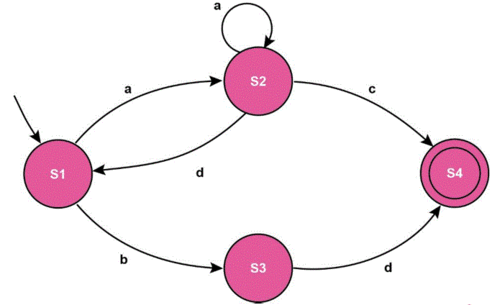
The symbols above can be used to create the following diagram:
This FSM defines the acceptable inputs of a language. If you start from the start state, and in correctly entering the input you finish on the accept/final state then the input is valid. However if no suitable path was possible, or you have run out of inputs before accessing the accept/final state, then the input is invalid.
Another way of representing Finite State Machines is through State Transition Tables. A State Transition Table lists all possible current states, all valid inputs that that particular state may receive, as well as what state the resulting transition leads to:
| Original State | Input | New State |
|---|---|---|
| S1 | a | S2 |
| S1 | b | S3 |
| S2 | a | S2 |
| S2 | d | S1 |
| S2 | c | S4 |
| S3 | d | S4 |
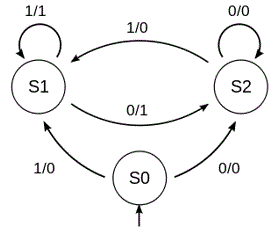
Mealy Machines
A finite state machine with an output is called a Mealy Machine. It will output a value based on the input. Transitions are usually labelled with both input and output. Complex Mealy Machines can have both multiple inputs and outputs. This means they can be designed to create ciphers.
Each transition is labeled: Input / Output
This can be represented in the following State Transition Table:
| Original State | Input | New State | Output |
|---|---|---|---|
| Example | Example | Example | Example |
| Example | Example | Example | Example |
| Example | Example | Example | Example |