Difference between revisions of "Regular Expressions"
(→Maths for Regular Expressions) |
|||
| Line 80: | Line 80: | ||
=Maths for Regular Expressions= | =Maths for Regular Expressions= | ||
| + | ==Basic set understanding== | ||
| + | Sets describe collections of things or values, such as numbers, animals or people. | ||
| + | In a set, each value occurs only once. For example, the value fox will occur only once in the set of animals. Just as the value 3 occurs only once in the element of all natural numbers, N. | ||
| + | The cardinality of a set refers to the number of elements it contains. | ||
| + | An empty set is written ∅ and its cardinality is 0. | ||
| + | Sets may be finite or infinite. For example, the set of people currently alive in the world will be finite, but the set of N is infinite. | ||
| + | A set may be countable or uncountable. A countable set is a set, whose elements can be matched with the set of natural numbers. In other words, it is possible to count the elements one-by-one. If a set is finite, it will always be countable. The best example of an uncountable set is R. It is impossible to match each element of R with an element of N. This is because there are not enough elements in N to match each one with an element of R. | ||
| + | |||
| + | ==Membership ∈ and its reverse ∉== | ||
| + | x ∈ S, x is an element of S. | ||
| + | |||
| + | Examples: | ||
| + | *x ∈ ℕ, meaning that x is an element of the set of natural numbers. For example, 3 ∈ ℕ. Whereas 3.5 ∉ ℕ | ||
| + | *x ∈ Q, meaning that x is an element of the set of rational numbers. Whereas pi ∉ Q | ||
| + | *x ∈ WorkingDays, meaning that x is an element of the set of all WorkingDays. For example, Monday ∈ WorkingDays. Whereas Saturday ∉ WorkingDays | ||
| + | *x ∈ WeekendDays, meaning that xis an element of the set of all WeekendDays. For example, Saturday ∈ WeekendDays. Whereas Monday ∉ WeekendDays | ||
Revision as of 19:16, 22 May 2017
A regular expression is a notation for defining all the valid strings of a formal language.
Contents
[hide]Examples of Regular Expression Notation
| Regular Expression | Meaning |
|---|---|
| a | Matches a string consisting of just the symbol a |
| b | Matches a string consisting of just the symbol b |
| ab | Matches a string consisting of the symbol a followed by the symbol b |
| a* | Matches a string consisting of zero or more a’s |
| a+ | Matches a string consisting of one or more a’s |
| abb? | Matches the string ab or the string abb. The ? symbol indicates zero or one of the preceding element |
| a|b | Matches a string consisting of the symbol a or the symbol b |
Precedence Rules
When using regular expressions, the rules of arithmetic precedence are as follows:
+ and * are done first
Concatenation (ie joining elements together) is done next
| comes last
More Examples
Examples of regular expressions using the alphabet {a, b, c}
- abc defines the language with only the string ‘abc’
- abc | cba defines the language with two strings’ abc’ and ‘cba’
- (a | b) c (a | b) gives four strings: ‘aca’, ‘acb’, ‘bca’, ‘bcb’
- a+ gives an infinite number of strings: ‘a’, ‘aa’, ‘aaa’, etc
- ab* gives an infinite number of strings: ‘a’, ‘ab’, ‘abb’, ‘abbb’, etc
- (ab)* gives an infinite number of strings: ‘’, ‘ab’, ‘abab’, ‘ababab’, etc
- (a | c)+ gives all possible strings of a and c (not including the empty string)
Regular expression meta-characters
| Symbol | Meaning | Example |
|---|---|---|
| │ | Used to separate alternatives | a│b (Means a or b) |
| ? | Used to denote zero or one of the preceding element | a? (0 or 1 as; matches with ‘’ & ‘a’) |
| * | Used to denote zero or more of the preceding element | a* (0 or more as; matches with ‘’, ‘a’, ‘aa’, etc.) |
| + | Used to denote one or more of the preceding element | a+ (1 or more as; matches with ‘a’, ‘aa”’etc.) |
| ( ) | Used to group characters together, to indicate the scope of another operator | (ab)* (Example 0 or more abs; matches with ‘’, ‘ab’, ‘abab’, etc. |
| [ ] | Another way of denoting alternatives (instead of vertical bar). Defines a character class | [ab] (means a or b) |
| \ | The escape character (this turns the metacharacter into an ordinary character) | a\* (the a character followed by the * character. Note: \ is needed as a* would mean zero or more as.) |
| ^ | Used to indicate the negation of a character class. Also used to match the position before the first character in a string | a[^bc] (a followed by a character that is not a b or c) ^abc will match with abc only if it is at the beginning of a string |
| $ | Used to match with the position after the last character in a string | abc$ (will match with abc only if it is at the end of a string) |
| . | Matches with any single character | a.a (will match with any string that has an a followed by any character followed by an a e.g. ‘aca’, ‘aba’) |
| - | Used to specify a range of values in a character class | [A-Z] (character in the range of A to Z) |
Regular Language
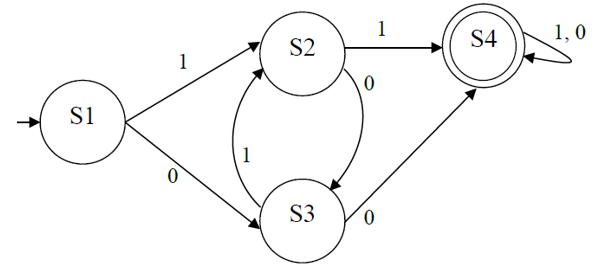
A regular language is a formal language that can be accepted by a finite state machine. Regular Expressions can also be specified using a FSM, an example question:
The FSM in below defines the language that allows all strings containing at least, either two consecutive 1s or two consecutive 0s. The strings 0110, 00 and 01011 are all accepted by the FSM and so are valid strings in the language. The strings 1010 and 01 are not accepted by the FSM and so are not valid strings in the language.
For 3 marks you need to write the regular expression that matches this FSM.
Maths for Regular Expressions
Basic set understanding
Sets describe collections of things or values, such as numbers, animals or people. In a set, each value occurs only once. For example, the value fox will occur only once in the set of animals. Just as the value 3 occurs only once in the element of all natural numbers, N. The cardinality of a set refers to the number of elements it contains. An empty set is written ∅ and its cardinality is 0. Sets may be finite or infinite. For example, the set of people currently alive in the world will be finite, but the set of N is infinite. A set may be countable or uncountable. A countable set is a set, whose elements can be matched with the set of natural numbers. In other words, it is possible to count the elements one-by-one. If a set is finite, it will always be countable. The best example of an uncountable set is R. It is impossible to match each element of R with an element of N. This is because there are not enough elements in N to match each one with an element of R.
Membership ∈ and its reverse ∉
x ∈ S, x is an element of S.
Examples:
- x ∈ ℕ, meaning that x is an element of the set of natural numbers. For example, 3 ∈ ℕ. Whereas 3.5 ∉ ℕ
- x ∈ Q, meaning that x is an element of the set of rational numbers. Whereas pi ∉ Q
- x ∈ WorkingDays, meaning that x is an element of the set of all WorkingDays. For example, Monday ∈ WorkingDays. Whereas Saturday ∉ WorkingDays
- x ∈ WeekendDays, meaning that xis an element of the set of all WeekendDays. For example, Saturday ∈ WeekendDays. Whereas Monday ∉ WeekendDays