Difference between revisions of "De Morgan's Law"
(→Example 4) |
(→How to apply) |
||
| Line 23: | Line 23: | ||
===Example 4=== | ===Example 4=== | ||
<math> (\overline{A} + B) . \overline{(A + (\overline{B +A})}) </math> | <math> (\overline{A} + B) . \overline{(A + (\overline{B +A})}) </math> | ||
| + | |||
| + | ===Example 5=== | ||
| + | <math> \overline{\overline{(\overline{A}+A.(A+B))} + (B . C)} </math> | ||
Revision as of 13:53, 9 May 2018
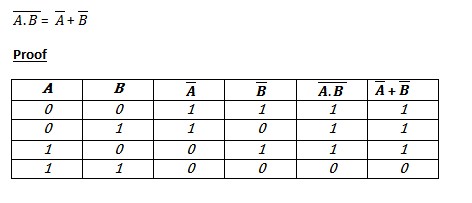
DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements. They can be easily remembered by "break the line, change the sign". The following image is how to prove De Morgan's Law...
The Process
Step 1 - Reverse the sign
Step 2 - Negate each term
Step 3 - Negate the whole expression
How to apply
Example 1
Example 2
Example 3
Example 4
Example 5