Difference between revisions of "Shortest Path"
m (Fixed Link) |
(→Overview) |
||
| (11 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Overview== | ||
| + | <youtube>https://www.youtube.com/watch?v=HXINXtriDQc&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E&index=9</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=HXINXtriDQc&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E&index=9 | ||
| + | |||
| + | ===TRC PowerPoints=== | ||
| + | [https://studentthomrothac-my.sharepoint.com/:p:/g/personal/wayne_jones_thomroth_ac_uk/EXvXtaURUkdKgDtfPSnImvoBt06zbZhcItJI5QOZRdjgwg?e=te0OrQ Example 1] | ||
| + | |||
| + | [https://studentthomrothac-my.sharepoint.com/:p:/g/personal/wayne_jones_thomroth_ac_uk/EXRkeEPokjZCuVrZzVB0mY0BKTBsuIQjzjUXpcaXcHBLqA?e=gftdjY Example 2] | ||
| + | |||
| + | ==Dijkstra== | ||
The shortest path is usually found by ''[https://www.youtube.com/watch?v=gdmfOwyQlcI Dijkstra's algorithm]''. | The shortest path is usually found by ''[https://www.youtube.com/watch?v=gdmfOwyQlcI Dijkstra's algorithm]''. | ||
The algorithm functions as follows: | The algorithm functions as follows: | ||
| − | + | ||
| − | + | '''Step 1''' Give the permanent label 0 to the starting vertex. | |
| − | + | ||
| − | + | '''Step 2''' Give temporary labels to each vertex that is connected directly to the starting vertex. | |
| − | + | ||
| + | '''Step 3''' Find the vertex with the smallest temporary label, number it and make it permanent. | ||
| + | |||
| + | '''Step 4''' Give temporary labels to each vertex that is connected directly to the previous vertex. Then find the vertex with the smallest temporary label, number it and make it permanent. | ||
| + | |||
| + | '''Step 5''' Repeat Step 4 until you have given a permanent label to the finishing vertex. | ||
| + | |||
| + | '''Step 6''' Use the permanent labels to trace back through the network to find the shortest path. | ||
| + | |||
| + | '''Step 7''' The shortest path is found by tracing back in such a way that an edge is only included if its distance equals the change in label values. | ||
| + | |||
| + | |||
| + | ==Example== | ||
| + | This is the starting graph and values: | ||
| + | |||
| + | [[File:Shortest path eg start.gif|600px]] | ||
| + | |||
| + | The stages to identify the shortest path from '''St. Austell''' to '''Launceston''': | ||
| + | |||
| + | [[File:Shortest path example.gif|800px]] | ||
| + | |||
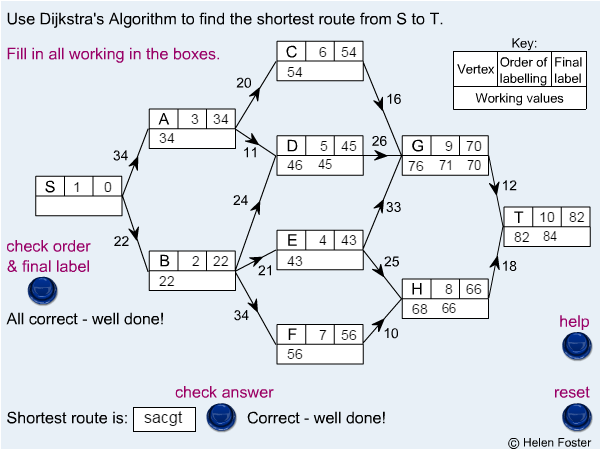
| + | ==Further Example== | ||
| + | [[File:Dijkstra.png]] | ||
Latest revision as of 11:48, 17 September 2018
Overview
https://www.youtube.com/watch?v=HXINXtriDQc&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E&index=9
TRC PowerPoints
Dijkstra
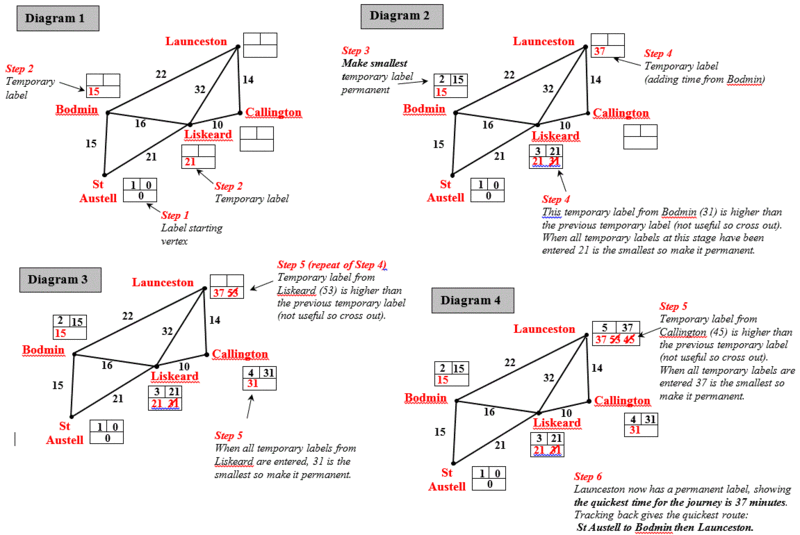
The shortest path is usually found by Dijkstra's algorithm. The algorithm functions as follows:
Step 1 Give the permanent label 0 to the starting vertex.
Step 2 Give temporary labels to each vertex that is connected directly to the starting vertex.
Step 3 Find the vertex with the smallest temporary label, number it and make it permanent.
Step 4 Give temporary labels to each vertex that is connected directly to the previous vertex. Then find the vertex with the smallest temporary label, number it and make it permanent.
Step 5 Repeat Step 4 until you have given a permanent label to the finishing vertex.
Step 6 Use the permanent labels to trace back through the network to find the shortest path.
Step 7 The shortest path is found by tracing back in such a way that an edge is only included if its distance equals the change in label values.
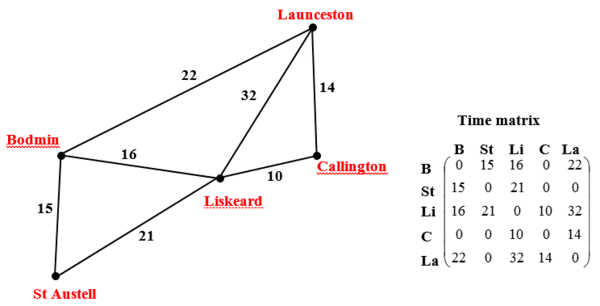
Example
This is the starting graph and values:
The stages to identify the shortest path from St. Austell to Launceston: