Difference between revisions of "Shortest Path"
(→Overview) |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Overview== | ||
| + | <youtube>https://www.youtube.com/watch?v=HXINXtriDQc&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E&index=9</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=HXINXtriDQc&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E&index=9 | ||
| + | |||
| + | ===TRC PowerPoints=== | ||
| + | [https://studentthomrothac-my.sharepoint.com/:p:/g/personal/wayne_jones_thomroth_ac_uk/EXvXtaURUkdKgDtfPSnImvoBt06zbZhcItJI5QOZRdjgwg?e=te0OrQ Example 1] | ||
| + | |||
| + | [https://studentthomrothac-my.sharepoint.com/:p:/g/personal/wayne_jones_thomroth_ac_uk/EXRkeEPokjZCuVrZzVB0mY0BKTBsuIQjzjUXpcaXcHBLqA?e=gftdjY Example 2] | ||
| + | |||
| + | ==Dijkstra== | ||
The shortest path is usually found by ''[https://www.youtube.com/watch?v=gdmfOwyQlcI Dijkstra's algorithm]''. | The shortest path is usually found by ''[https://www.youtube.com/watch?v=gdmfOwyQlcI Dijkstra's algorithm]''. | ||
The algorithm functions as follows: | The algorithm functions as follows: | ||
| Line 14: | Line 25: | ||
'''Step 6''' Use the permanent labels to trace back through the network to find the shortest path. | '''Step 6''' Use the permanent labels to trace back through the network to find the shortest path. | ||
| − | '''Step 7''' The shortest path is found by tracing back in such a way that an edge is only included if | + | '''Step 7''' The shortest path is found by tracing back in such a way that an edge is only included if its distance equals the change in label values. |
| − | |||
| Line 21: | Line 31: | ||
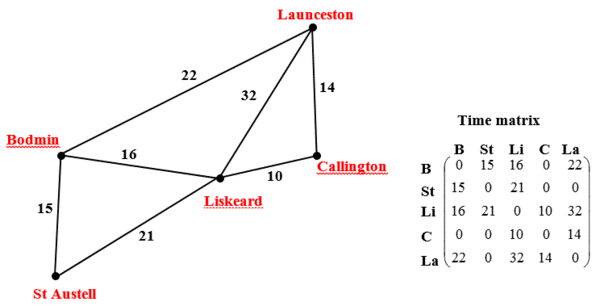
This is the starting graph and values: | This is the starting graph and values: | ||
| − | [[File:Shortest path eg start.gif]] | + | [[File:Shortest path eg start.gif|600px]] |
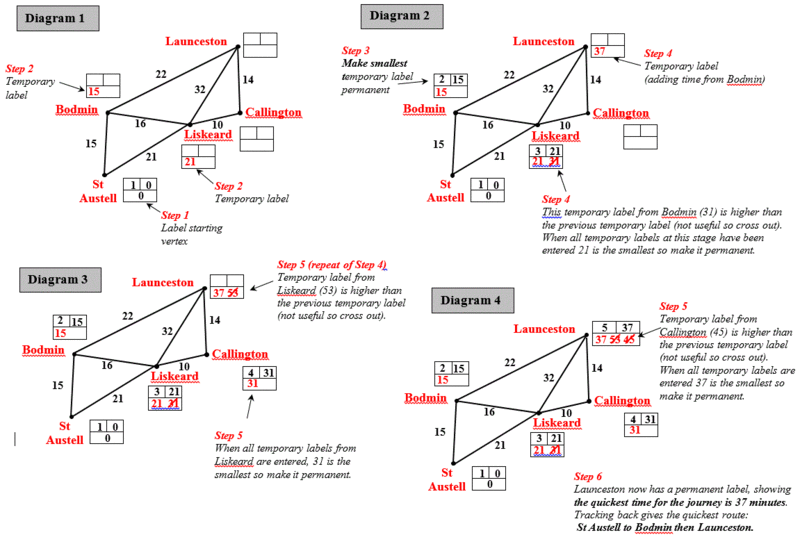
| − | The stages to identify the shortest path: | + | The stages to identify the shortest path from '''St. Austell''' to '''Launceston''': |
[[File:Shortest path example.gif|800px]] | [[File:Shortest path example.gif|800px]] | ||
Latest revision as of 11:48, 17 September 2018
Overview
https://www.youtube.com/watch?v=HXINXtriDQc&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E&index=9
TRC PowerPoints
Dijkstra
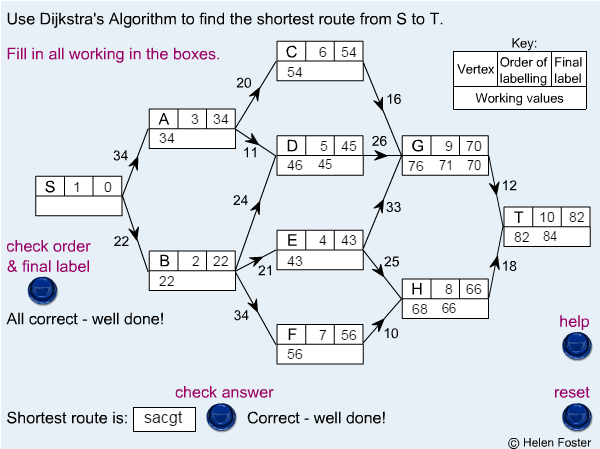
The shortest path is usually found by Dijkstra's algorithm. The algorithm functions as follows:
Step 1 Give the permanent label 0 to the starting vertex.
Step 2 Give temporary labels to each vertex that is connected directly to the starting vertex.
Step 3 Find the vertex with the smallest temporary label, number it and make it permanent.
Step 4 Give temporary labels to each vertex that is connected directly to the previous vertex. Then find the vertex with the smallest temporary label, number it and make it permanent.
Step 5 Repeat Step 4 until you have given a permanent label to the finishing vertex.
Step 6 Use the permanent labels to trace back through the network to find the shortest path.
Step 7 The shortest path is found by tracing back in such a way that an edge is only included if its distance equals the change in label values.
Example
This is the starting graph and values:
The stages to identify the shortest path from St. Austell to Launceston: