Difference between revisions of "De Morgan's Law"
(Created page with "DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements. They can be easily remembered by "break the line, change the sign". The following image is how to...") |
(→Video) |
||
| (33 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
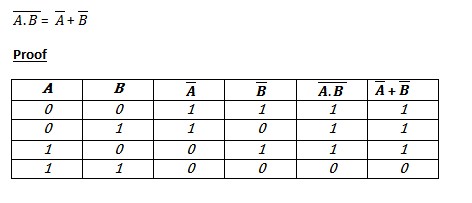
DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements. They can be easily remembered by "break the line, change the sign". The following image is how to prove De Morgan's Law... | DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements. They can be easily remembered by "break the line, change the sign". The following image is how to prove De Morgan's Law... | ||
[[File:capture3.jpg]] | [[File:capture3.jpg]] | ||
| + | |||
| + | Further explanation: | ||
| + | |||
| + | ===Video=== | ||
| + | <youtube>https://www.youtube.com/watch?v=HoH0PrS3WNI&list=PLCiOXwirraUA9HyHoqOaGBU_k6nBRCb22&index=6</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=HoH0PrS3WNI&list=PLCiOXwirraUA9HyHoqOaGBU_k6nBRCb22&index=6 | ||
| + | |||
| + | ===TRC Video=== | ||
| + | <youtube>https://www.youtube.com/watch?v=O3w4yGY90SU</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=O3w4yGY90SU | ||
| + | |||
| + | ==The Process== | ||
| + | |||
| + | ===Step 1 - Reverse the sign=== | ||
| + | ===Step 2 - Negate each term=== | ||
| + | ===Step 3 - Negate the whole expression=== | ||
| + | |||
| + | It is recommended to "Break the longest line" when applying De Morgan's law. | ||
| + | |||
| + | You can often treat a whole set of brackets as a single term. | ||
| + | |||
| + | ==How to apply== | ||
| + | ===Example 1=== | ||
| + | |||
| + | |||
| + | <math> \overline{(\overline{A+B})+B} </math> | ||
| + | |||
| + | Now we use De Morgan's law to the whole equation and we treat A+B as one. | ||
| + | |||
| + | <math> (A+B).\overline {B} </math> | ||
| + | |||
| + | <math> \overline {B}.A + (\overline{B}.B) </math> | ||
| + | |||
| + | <math> \overline{B}.A + 0 </math> | ||
| + | |||
| + | <math> \overline{B}.A </math> | ||
| + | |||
| + | ===Example 2=== | ||
| + | <math>(\overline{A+\overline{B}).\overline{A}}</math> | ||
| + | |||
| + | ===Example 3=== | ||
| + | <math> \overline{(\overline{A+B}).\overline{A}} </math> | ||
| + | |||
| + | Simplifying by using De Morgan's Law: | ||
| + | |||
| + | 1. Swap the sign: | ||
| + | |||
| + | <math> \overline{(\overline{A+B})+\overline{A}} </math> | ||
| + | |||
| + | 2. Negate each term: | ||
| + | |||
| + | <math> \overline{\overline{\overline{(A+B)}}+\overline{\overline{A}}} </math> | ||
| + | |||
| + | 3. Negate the whole Expression: | ||
| + | |||
| + | <math> \overline{\overline{\overline{\overline{(A+B)}}+\overline{\overline{A}}}} </math> | ||
| + | |||
| + | Or: | ||
| + | |||
| + | <math>(A+B)+A </math> | ||
| + | |||
| + | Using Redundancy law this expression can be simplified to: | ||
| + | |||
| + | <math> A </math> | ||
| + | |||
| + | This is because if A is 1, the output will always be 1, regardless of the value of B. | ||
| + | |||
| + | ===Example 4=== | ||
| + | <math> (\overline{A} + B) . \overline{(A + (\overline{B + A})}) </math> | ||
| + | |||
| + | Applying De Morgan's law to the inner bracket | ||
| + | |||
| + | <math> (\overline{A} + B) . \overline{(A + (B + A)}) </math> Inverting the not gate above the bracket | ||
| + | |||
| + | <math> (\overline{A} + B) . \overline{(A + (B . A)}) </math> Swapping signs | ||
| + | |||
| + | <math> (\overline{A} + B) . \overline{(A + (\overline{B} . \overline{A})}) </math> Inverting not gates above terms | ||
| + | |||
| + | Applying De Morgan's law to the right bracket | ||
| + | |||
| + | <math> (\overline{A} + B) . (A + (\overline{B} . \overline{A})) </math> Inverting the top not gate | ||
| + | |||
| + | <math> (\overline{A} + B) . (A . (\overline{B} + \overline{A})) </math> Swapping signs | ||
| + | |||
| + | <math> (\overline{A} + B) . (\overline{A} . (B + A)) </math> Inverting not gates above terms | ||
| + | |||
| + | Now that it is easier to simplify, we can do that | ||
| + | |||
| + | <math> (\overline{A} + B) . ((\overline{A} . B) + (\overline{A} . A))) </math> Applying the distributive law | ||
| + | |||
| + | <math> (\overline{A} + B) . ((\overline{A} . B) + 0)) </math> Applying an identity law | ||
| + | |||
| + | <math> (\overline{A} + B) . (\overline{A} . B) </math> | ||
| + | |||
| + | <math> (\overline{A} . \overline{A} . B) + (B . \overline{A} . B) </math> Expand the brackets | ||
| + | |||
| + | <math> (\overline{A} . B) + (\overline{A} . B) </math> Use identity <math> X . X = X </math> | ||
| + | |||
| + | <math> \overline{A} . B </math> Use identity <math> X + X = X </math> | ||
| + | |||
| + | ===Example 5=== | ||
| + | <math> \overline{\overline{(\overline{A}+A.(A+B))} + (B . C)} </math> | ||
| + | |||
| + | ===Example 6=== | ||
| + | <math> \overline{\overline{(A+A.(\overline{A+B}))} + (B . C)} </math> | ||
| + | |||
| + | ===Example 7=== | ||
| + | <math> \overline{(\overline{A}+A.(A+B))} + \overline{(B.C)} </math> | ||
| + | |||
| + | <math> \overline{(\overline{A}+A+A.B)}+(\overline{B}+\overline{C}) </math> | ||
| + | |||
| + | <math> (A.\overline{A}.\overline{A}+\overline{B})+(\overline{B}+\overline{C}) </math> | ||
| + | |||
| + | <math> (A.\overline{A}+\overline{B})+(\overline{B}+\overline{C}) </math> | ||
| + | |||
| + | <math> (0+\overline{B})+(\overline{B}+\overline{C}) </math> | ||
| + | |||
| + | <math> \overline {B}+(\overline{B}+\overline{C}) </math> | ||
| + | |||
| + | <math> \overline{C}+(\overline{B}+\overline{B}) </math> | ||
| + | |||
| + | <math> \overline{B}+\overline{C} </math> | ||
Latest revision as of 09:05, 23 August 2023
DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements. They can be easily remembered by "break the line, change the sign". The following image is how to prove De Morgan's Law...
Further explanation:
Video
https://www.youtube.com/watch?v=HoH0PrS3WNI&list=PLCiOXwirraUA9HyHoqOaGBU_k6nBRCb22&index=6
TRC Video
https://www.youtube.com/watch?v=O3w4yGY90SU
The Process
Step 1 - Reverse the sign
Step 2 - Negate each term
Step 3 - Negate the whole expression
It is recommended to "Break the longest line" when applying De Morgan's law.
You can often treat a whole set of brackets as a single term.
How to apply
Example 1
Now we use De Morgan's law to the whole equation and we treat A+B as one.
Example 2
Example 3
Simplifying by using De Morgan's Law:
1. Swap the sign:
2. Negate each term:
3. Negate the whole Expression:
Or:
Using Redundancy law this expression can be simplified to:
This is because if A is 1, the output will always be 1, regardless of the value of B.
Example 4
Applying De Morgan's law to the inner bracket
Inverting the not gate above the bracket
Swapping signs
Inverting not gates above terms
Applying De Morgan's law to the right bracket
Inverting the top not gate
Swapping signs
Inverting not gates above terms
Now that it is easier to simplify, we can do that
Applying the distributive law
Applying an identity law
Expand the brackets
Use identity
Use identity
Example 5
Example 6
Example 7