Difference between revisions of "Vectors"
(→Adding Vectors) |
|||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Vectors can be represented and used in varying ways within computer science. A vector for example can be a data structure used to store values, a vector could also be a function which maps one value to another. The final representation is to define geometric shapes, such has vector graphics. | Vectors can be represented and used in varying ways within computer science. A vector for example can be a data structure used to store values, a vector could also be a function which maps one value to another. The final representation is to define geometric shapes, such has vector graphics. | ||
| + | ===Resources=== | ||
<youtube>https://www.youtube.com/watch?v=Wc3bswImxA4&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=13</youtube> | <youtube>https://www.youtube.com/watch?v=Wc3bswImxA4&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=13</youtube> | ||
https://www.youtube.com/watch?v=Wc3bswImxA4&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=13 | https://www.youtube.com/watch?v=Wc3bswImxA4&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=13 | ||
| + | |||
| + | ===TRC Video=== | ||
| + | <youtube>https://www.youtube.com/watch?v=_asvSYM2l8A</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=_asvSYM2l8A | ||
==Data Structure== | ==Data Structure== | ||
| Line 12: | Line 18: | ||
==Vectors as a function== | ==Vectors as a function== | ||
A function essentially maps an input to an output, for example the function f(x) = x2 will take the input (x) and map it to the squared value of x. A vector can therefore be used to represent a function: | A function essentially maps an input to an output, for example the function f(x) = x2 will take the input (x) and map it to the squared value of x. A vector can therefore be used to represent a function: | ||
| + | |||
| + | * F is the function | ||
| + | * S is the set of possible inputs | ||
| + | * R is the set of possible outputs | ||
Therefore F: S → R | Therefore F: S → R | ||
| + | |||
==Vectors as arrows== | ==Vectors as arrows== | ||
| Line 34: | Line 45: | ||
=Vector Calculations= | =Vector Calculations= | ||
For calculations break the vector into x & y components: | For calculations break the vector into x & y components: | ||
| + | [[File:Vector xy.png]] | ||
So vector A has an x component and a y component, ie Ax & Ay , and Each component will be the number of units. | So vector A has an x component and a y component, ie Ax & Ay , and Each component will be the number of units. | ||
==Adding Vectors== | ==Adding Vectors== | ||
| − | [[File:Vector addition.png | + | [[File:Vector addition.png]] |
| + | |||
To add two vectors together you can place the start of your second vector at the end of your first. The line from the start of the first vector to the end of you second vector should be the result of adding them together. | To add two vectors together you can place the start of your second vector at the end of your first. The line from the start of the first vector to the end of you second vector should be the result of adding them together. | ||
| Line 50: | Line 63: | ||
==Subtracting Vectors== | ==Subtracting Vectors== | ||
| + | [[File:Vectors subtraction.png]] | ||
| + | |||
Using a similar method to the one shown in vector addition, you break each vector into x & y components and subtract the Bx value from the Ax value, and subtract the By value from the Ay value. | Using a similar method to the one shown in vector addition, you break each vector into x & y components and subtract the Bx value from the Ax value, and subtract the By value from the Ay value. | ||
| Line 62: | Line 77: | ||
==Calculating the Magnitude== | ==Calculating the Magnitude== | ||
You can use Pythagoras to calculate the magnitude of a vector: | You can use Pythagoras to calculate the magnitude of a vector: | ||
| + | [[File:Vector magnitude.png]] | ||
| + | |||
For example the vector Z = (6, 8): | For example the vector Z = (6, 8): | ||
| Line 68: | Line 85: | ||
==Vector multiplication by scalar== | ==Vector multiplication by scalar== | ||
One of the key concepts of Vector Graphics is that the image can be mathematically scaled to any size and still retain the quality of the graphic. Any vector can be scaled by multiplying both the x and y components by the same scalar. | One of the key concepts of Vector Graphics is that the image can be mathematically scaled to any size and still retain the quality of the graphic. Any vector can be scaled by multiplying both the x and y components by the same scalar. | ||
| + | [[File:Vector scalar.png]] | ||
For example the vector M = (7, 3) and we want to multiply it by the scalar 3: | For example the vector M = (7, 3) and we want to multiply it by the scalar 3: | ||
| Line 73: | Line 91: | ||
The new vector A will still point in the same direction but it will be 3 times longer. | The new vector A will still point in the same direction but it will be 3 times longer. | ||
| − | |||
==Dot Product== | ==Dot Product== | ||
Latest revision as of 09:24, 23 August 2023
Vectors can be represented and used in varying ways within computer science. A vector for example can be a data structure used to store values, a vector could also be a function which maps one value to another. The final representation is to define geometric shapes, such has vector graphics.
Contents
[hide]Resources
https://www.youtube.com/watch?v=Wc3bswImxA4&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=13
TRC Video
https://www.youtube.com/watch?v=_asvSYM2l8A
Data Structure
Values stored within a list. Often a one dimensional array where each value can be accessed by its location.
A dictionary could alternatively be used with the key used as the index of the data structure.
Vectors as a function
A function essentially maps an input to an output, for example the function f(x) = x2 will take the input (x) and map it to the squared value of x. A vector can therefore be used to represent a function:
- F is the function
- S is the set of possible inputs
- R is the set of possible outputs
Therefore F: S → R
Vectors as arrows
https://www.youtube.com/watch?v=ZC8buHPrSAY&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=14
A vector is a combination of 3 things:
- A positive number called its magnitude
- A direction in space
- A sense giving more precise idea of direction
Two vectors are equal if they have the same magnitude, the same direction (ie parallel), and the same sense: In the diagram above we can say:
If two vectors have the same length and are parallel but have opposite senses then one is the negative of the other:
In the diagram above we can say:
Vector Calculations
For calculations break the vector into x & y components:
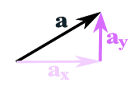
So vector A has an x component and a y component, ie Ax & Ay , and Each component will be the number of units.
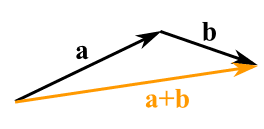
Adding Vectors
To add two vectors together you can place the start of your second vector at the end of your first. The line from the start of the first vector to the end of you second vector should be the result of adding them together.
You can work this out mathematically by adding together the x component of each vector and adding together the y component of each vector.
So adding together vector A=(8, 13) and vector B=(26, 7) is essentially:
A+B = (Ax +Bx , Ay + By)
A+B = (8 + 26, 13 + 7) = (34, 20)
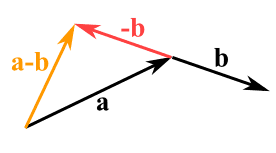
Subtracting Vectors
Using a similar method to the one shown in vector addition, you break each vector into x & y components and subtract the Bx value from the Ax value, and subtract the By value from the Ay value.
So if vector K= (4,5) and vector V = (12,2), V – K would be:
V - K = (12, 2) – (4, 5) = (12 – 4, 2 – 5) = (8, -3)
Alternatively you could also say that:
V - K = V + -K
Calculating the Magnitude
You can use Pythagoras to calculate the magnitude of a vector:
![]()
For example the vector Z = (6, 8):
So the |Z| = √(62 + 82) = √(36 + 64) = √(100) = 10
Vector multiplication by scalar
One of the key concepts of Vector Graphics is that the image can be mathematically scaled to any size and still retain the quality of the graphic. Any vector can be scaled by multiplying both the x and y components by the same scalar.
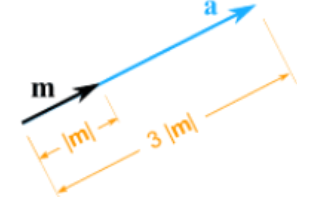
For example the vector M = (7, 3) and we want to multiply it by the scalar 3: A = 3m = (3 * 7, 3 * 3) = (21, 9)
The new vector A will still point in the same direction but it will be 3 times longer.
Dot Product
https://www.youtube.com/watch?v=7o6kgVUSE8s&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=16
This is a process of combining two vectors to calculate a single number. This is achieved by multiplying the two x components and the two y components and then adding these two values together.
So:
A.B = (Ax * Bx) + (Ay * By)
If A = (3, 5) and B = (7, 2)
A.B = (3 * 7) + (5 * 2) = 21 + 10 = 31
This would also work in three dimensions:
If A = (5, 3, 2) and B = (2, 7, 4)
A.B = (5 * 2) + (3 * 7) + (2 * 4) = (10) + (21) + (8) = 39
https://www.youtube.com/watch?v=a9VMJ7-AyFg&index=17&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW
Convex Combinations
https://www.youtube.com/watch?v=6N_caSzNpkc&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=15
Convex Hull: Can be visualized as the space enclosed by a rubber band being stretched around a set of direction vectors.
Convex Combinations is a method of multiplying vectors that produces a resulting vector within the convex hull, which is a spatial representation of the vector space between the two vectors, a good example of this would be the field of view on a camera in a game. Mathematically,to perform a convex combination, you will be multiplying one vector either by a scalar, or by another vector.
This could be represented as:
D = αAB + βAC
AB and AC are the two direction vectors
α and β represent the real number that each vector will be multiplied by
α and β must both be greater than or equal to 0 and α + β must equal 1.
D will then fall within the vector space.