Difference between revisions of "Graphs"
Mfrederick (talk | contribs) (→Adjacency Matrix) |
(→Summary) |
||
| (31 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | |||
==What is a graph== | ==What is a graph== | ||
| − | [[File:Graph- | + | [[File:Graph-4.jpg|300px]] |
| + | |||
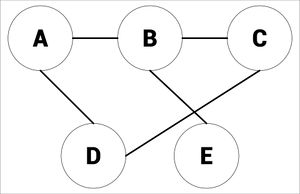
A graph is an abstract data structure. It can be used to solve routine problems. | A graph is an abstract data structure. It can be used to solve routine problems. | ||
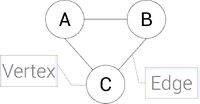
Vertices connected by an edge (see picture) are called Neighbours. | Vertices connected by an edge (see picture) are called Neighbours. | ||
| − | The degree of a vertex is how many things are connected to it, in the picture, there would be 2. | + | The degree of a vertex is how many things are connected to it, in the picture below, there would be 2: |
| + | |||
| + | [[File:Graph-1.jpg|200px]] | ||
Edges can also be called connectors and vertex can also be called nodes or entries. | Edges can also be called connectors and vertex can also be called nodes or entries. | ||
| + | |||
| + | <youtube>https://www.youtube.com/watch?v=PMPMDZqeipw&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=7</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=PMPMDZqeipw&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=7 | ||
==Terms== | ==Terms== | ||
===weighted graph=== | ===weighted graph=== | ||
| + | Each edge/arc has an associated value, which can be used for distance, cost and so on. | ||
===vertex/node=== | ===vertex/node=== | ||
| + | An entity, location within the graph (represented by a circle). | ||
===edge/arc=== | ===edge/arc=== | ||
| + | A connection between two vertex/nodes | ||
===undirected graph=== | ===undirected graph=== | ||
| + | You can travel either direction on an edge/arc. For example an edge between A & B allows movement from A to B and from B to A. | ||
===directed graph=== | ===directed graph=== | ||
| − | ==Adjacency | + | Each edge/arc will have an arrow to indicate the direction of travel. This will require additional edges to cover both directions. |
| + | |||
| + | ==Adjacency List== | ||
[[File:Graph-2.jpg|thumb|300px]] | [[File:Graph-2.jpg|thumb|300px]] | ||
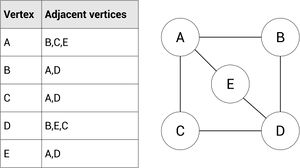
An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other. | An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other. | ||
| + | |||
| + | Each node will therefore have a list of the nodes it is connected to. There is no way of recording any weightings so this will only work with un-weighted graphs. | ||
| + | |||
| + | <br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 25: | Line 43: | ||
<br /> | <br /> | ||
| − | ==Adjacency | + | ==Adjacency Matrix== |
[[File:Graph-3.jpg|thumb|300px]] | [[File:Graph-3.jpg|thumb|300px]] | ||
| − | This is a list shown in binary for the values that are going to be connected. It usually helps to transfer the matrices into a list first before you turn it into a graph | + | This is a list shown in binary for the values that are going to be connected. It usually helps to transfer the matrices into a list first before you turn it into a graph to make things easier. '0' means the edge is not connected and '1' will mean it is connected. |
| + | |||
| + | The simple 1's & 0's could be replaced with '0' if it is not connected and a value to represent the weight if it is connected. | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
==Comparison of List VS Matrix== | ==Comparison of List VS Matrix== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! List!! Matrix | ||
| + | |- | ||
| + | | for a node you need to look at each edge it is connected to || Its quicker to find an edge because you go directly to the single edge | ||
| + | |- | ||
| + | | Less space, no wastage || Stores information about each possible edge whether it is connected or not | ||
| + | |- | ||
| + | | Can't be a weighted graph, no way to store the value || Can be a weighted graph, the value stored in the matrix could be the weight | ||
| + | |} | ||
| + | |||
| + | ===Summary=== | ||
| + | It is always better to use an adjacency list when you have many nodes but few edges. | ||
| + | |||
| + | It is always better to use an adjacency matrix when you have many edges. | ||
| + | |||
| + | =='''Quiz'''== | ||
| + | ===Question 1=== | ||
| + | ===Question 2=== | ||
| + | ===Question 3=== | ||
| + | ===Question 4=== | ||
| + | ===Question 5=== | ||
| + | ===Question 6=== | ||
| + | ===Question 7=== | ||
| + | ===Question 8=== | ||
| + | ===Question 9=== | ||
| + | ===Question 10=== | ||
| + | ===Question 11=== | ||
| + | ===Question 12=== | ||
Latest revision as of 10:29, 16 December 2024
Contents
[hide]What is a graph
A graph is an abstract data structure. It can be used to solve routine problems.
Vertices connected by an edge (see picture) are called Neighbours.
The degree of a vertex is how many things are connected to it, in the picture below, there would be 2:
Edges can also be called connectors and vertex can also be called nodes or entries.
https://www.youtube.com/watch?v=PMPMDZqeipw&list=PLCiOXwirraUD0G290WrVKpVYd3leGRRMW&index=7
Terms
weighted graph
Each edge/arc has an associated value, which can be used for distance, cost and so on.
vertex/node
An entity, location within the graph (represented by a circle).
edge/arc
A connection between two vertex/nodes
undirected graph
You can travel either direction on an edge/arc. For example an edge between A & B allows movement from A to B and from B to A.
directed graph
Each edge/arc will have an arrow to indicate the direction of travel. This will require additional edges to cover both directions.
Adjacency List
An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other.
Each node will therefore have a list of the nodes it is connected to. There is no way of recording any weightings so this will only work with un-weighted graphs.
Adjacency Matrix
This is a list shown in binary for the values that are going to be connected. It usually helps to transfer the matrices into a list first before you turn it into a graph to make things easier. '0' means the edge is not connected and '1' will mean it is connected.
The simple 1's & 0's could be replaced with '0' if it is not connected and a value to represent the weight if it is connected.
Comparison of List VS Matrix
| List | Matrix |
|---|---|
| for a node you need to look at each edge it is connected to | Its quicker to find an edge because you go directly to the single edge |
| Less space, no wastage | Stores information about each possible edge whether it is connected or not |
| Can't be a weighted graph, no way to store the value | Can be a weighted graph, the value stored in the matrix could be the weight |
Summary
It is always better to use an adjacency list when you have many nodes but few edges.
It is always better to use an adjacency matrix when you have many edges.