Difference between revisions of "Intractable Problems"
(→Halting Problem Example) |
(→TRC PowerPoints) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | =Overview= | ||
| + | |||
| + | <youtube>https://www.youtube.com/watch?v=LJvtQRtOUMA&index=5&list=PLCiOXwirraUDwnyalzSD1aCvtUnw_UHkd</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=LJvtQRtOUMA&index=5&list=PLCiOXwirraUDwnyalzSD1aCvtUnw_UHkd | ||
| + | |||
| + | ===TRC Video=== | ||
| + | <youtube>https://www.youtube.com/watch?v=Tm4RtMRZGMM</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=Tm4RtMRZGMM | ||
| + | |||
=Algorithmic Problems= | =Algorithmic Problems= | ||
| Line 6: | Line 17: | ||
*An algorithm such that a computer following it would be actually thinking | *An algorithm such that a computer following it would be actually thinking | ||
| − | Any algorithm with a finite set of inputs is solvable, however algorithms with an Infinite sets of inputs are less accommodating and potential unsolvable. Overall Algorithmic problems may be solved by following a set of rules or steps. Non-Algorithmic problems cannot be solved by following a set of rules or steps. | + | Any algorithm with a finite set of inputs is solvable, however algorithms with an Infinite sets of inputs are less accommodating and potential unsolvable. Overall '''Algorithmic problems''' may be solved by following a set of rules or steps. '''Non-Algorithmic problems''' cannot be solved by following a set of rules or steps. |
| − | Algorithmic Problems Examples | + | ===Algorithmic Problems Examples=== |
*Find the square of a number | *Find the square of a number | ||
*How to make an omelette | *How to make an omelette | ||
| Line 14: | Line 25: | ||
*Find the average of a set of numbers | *Find the average of a set of numbers | ||
| − | Non-Algorithmic Problems Examples | + | ===Non-Algorithmic Problems Examples=== |
*What is the meaning of life? | *What is the meaning of life? | ||
*Am I in love? | *Am I in love? | ||
| Line 33: | Line 44: | ||
Problems that have a reasonable (polynomial) time solutions are called '''tractable'''. | Problems that have a reasonable (polynomial) time solutions are called '''tractable'''. | ||
| − | Problems that have no reasonable ( | + | Problems that have no reasonable (exponential/factorial) time solutions are called '''intractable'''. |
Some intractable problems are solvable in a reasonable time for small inputs only, and the solution / algorithm doesn’t scale to larger inputs. Some intractable problems are solved everyday even though they are intractable. Such has routing algorithms, timetabling, resource scheduling. These tend to use a guessed solution to an intractable problem which can then be checked quickly. This is called heuristics, and his an example of a NP-type problem. | Some intractable problems are solvable in a reasonable time for small inputs only, and the solution / algorithm doesn’t scale to larger inputs. Some intractable problems are solved everyday even though they are intractable. Such has routing algorithms, timetabling, resource scheduling. These tend to use a guessed solution to an intractable problem which can then be checked quickly. This is called heuristics, and his an example of a NP-type problem. | ||
| Line 42: | Line 53: | ||
One example of an intractable problem, you have to travel from the starting city to all cities on the map and back to the starting city, for the lowest cost. | One example of an intractable problem, you have to travel from the starting city to all cities on the map and back to the starting city, for the lowest cost. | ||
| + | |||
| + | [[File:TSP.gif]] | ||
| + | |||
| + | |||
To calculate the number of possible routes, you can find the factorial of n-1 to tell you how many routes there are, however you can divide this by 2 because each route has an identical route in reverse: | To calculate the number of possible routes, you can find the factorial of n-1 to tell you how many routes there are, however you can divide this by 2 because each route has an identical route in reverse: | ||
So 5 cities will be: | So 5 cities will be: | ||
| − | + | *4! = 24 | |
| − | + | *24 / 2 = 12 routes | |
| + | |||
So 10 cities will be: | So 10 cities will be: | ||
| − | + | *9! = 362880 | |
| − | + | *362880 / 2 = 181440 routes | |
So 12 cities will be: | So 12 cities will be: | ||
| − | + | *11! = 39916800 | |
| − | + | *39916800 / 2 = 19958400 routes | |
=The Halting Problem= | =The Halting Problem= | ||
| Line 62: | Line 78: | ||
‘Is it possible to write a program that can tell given any program and its inputs and without executing the program, whether it will halt?’ | ‘Is it possible to write a program that can tell given any program and its inputs and without executing the program, whether it will halt?’ | ||
| − | A method to do this for any program has been proven to not exist. | + | A method to do this for any program has been proven to not exist. |
| + | |||
| + | <youtube>https://www.youtube.com/watch?v=iSShQcn6Bh0&index=6&list=PLCiOXwirraUDwnyalzSD1aCvtUnw_UHkd</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=iSShQcn6Bh0&index=6&list=PLCiOXwirraUDwnyalzSD1aCvtUnw_UHkd | ||
===Halting Problem Example=== | ===Halting Problem Example=== | ||
| − | <syntaxhighlight> | + | <syntaxhighlight lang=Bash> |
Input x | Input x | ||
| Line 87: | Line 107: | ||
*x = 15 | *x = 15 | ||
*x = 105 | *x = 105 | ||
| − | x | + | *x = positive integer |
Latest revision as of 09:03, 23 August 2023
Contents
Overview
https://www.youtube.com/watch?v=LJvtQRtOUMA&index=5&list=PLCiOXwirraUDwnyalzSD1aCvtUnw_UHkd
TRC Video
https://www.youtube.com/watch?v=Tm4RtMRZGMM
Algorithmic Problems
Some algorithms are impossible to write for example:
- An algorithm that can evaluate if another algorithm will work
- An algorithm such that a computer following it would be actually thinking
Any algorithm with a finite set of inputs is solvable, however algorithms with an Infinite sets of inputs are less accommodating and potential unsolvable. Overall Algorithmic problems may be solved by following a set of rules or steps. Non-Algorithmic problems cannot be solved by following a set of rules or steps.
Algorithmic Problems Examples
- Find the square of a number
- How to make an omelette
- How to negotiate a maze
- Find the average of a set of numbers
Non-Algorithmic Problems Examples
- What is the meaning of life?
- Am I in love?
- What is happiness?
Computability
If an algorithm can be constructed to solve a particular problem then that problem is computable. However if an algorithm cannot be constructed to solve a particular problem then that problem is non-computable.
Decision Problems
A decision problem is a yes/no algorithmic problem, it therefore requires a yes/no answer.
If a decision problem as an algorithmic solution it is said to be decidable. If a decision problem is non-computable it is said to be undecidable. ie its an algorithmic problem with no algorithm to solve it. The tiling problem is an example of an undecidable problem. An algorithm to say if any given number is prime is decidable.
Intractable / Tractable Problems
Problems that have a reasonable (polynomial) time solutions are called tractable.
Problems that have no reasonable (exponential/factorial) time solutions are called intractable.
Some intractable problems are solvable in a reasonable time for small inputs only, and the solution / algorithm doesn’t scale to larger inputs. Some intractable problems are solved everyday even though they are intractable. Such has routing algorithms, timetabling, resource scheduling. These tend to use a guessed solution to an intractable problem which can then be checked quickly. This is called heuristics, and his an example of a NP-type problem.
Heuristics uses knowledge and experience to make intelligent guesses, remember brute force will try solutions which knowledge and experience tell us aren’t workable or possible. The heuristic approach may also seek to find a suitable solution and not necessarily the perfect or ideal.
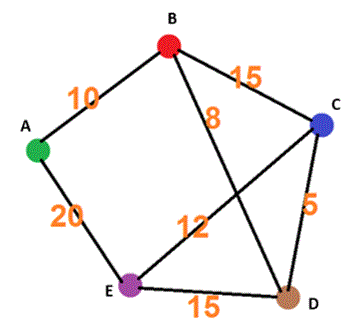
Travelling Salesman Problem
One example of an intractable problem, you have to travel from the starting city to all cities on the map and back to the starting city, for the lowest cost.
To calculate the number of possible routes, you can find the factorial of n-1 to tell you how many routes there are, however you can divide this by 2 because each route has an identical route in reverse:
So 5 cities will be:
- 4! = 24
- 24 / 2 = 12 routes
So 10 cities will be:
- 9! = 362880
- 362880 / 2 = 181440 routes
So 12 cities will be:
- 11! = 39916800
- 39916800 / 2 = 19958400 routes
The Halting Problem
When you run a program it will either run for awhile and then stop (halt), or get stuck in an infinite loop and crash the machine. If a program runs for a long time, do we conclude the program is stuck in a loop or that we have not allowed enough time for the program to calculate its output.
The halting problem asks:
‘Is it possible to write a program that can tell given any program and its inputs and without executing the program, whether it will halt?’
A method to do this for any program has been proven to not exist.
https://www.youtube.com/watch?v=iSShQcn6Bh0&index=6&list=PLCiOXwirraUDwnyalzSD1aCvtUnw_UHkd
Halting Problem Example
Input x
While x not equal to 1
If x is even
x = x / 2
else
x = (x *3) +1
End While
Will this terminate with the following input:
- x = 15
- x = 105
- x = positive integer