Difference between revisions of "Logic Gates"
(→And Gates) |
|||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
=And Gates= | =And Gates= | ||
| Line 28: | Line 26: | ||
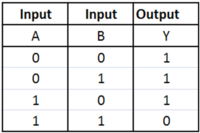
An OR gate is when either of the values can be true, and the output shall always be true in that instance. The images below shows what the OR gate looks like, and the table shows all possible outcomes. | An OR gate is when either of the values can be true, and the output shall always be true in that instance. The images below shows what the OR gate looks like, and the table shows all possible outcomes. | ||
| − | [[File:OrGate.gif]] [[File:Image002.gif]] | + | [[File:OrGate.gif]] |
| + | |||
| + | ===Truth Table=== | ||
| + | [[File:Image002.gif]] | ||
| + | |||
| + | ===Boolean Equation=== | ||
| + | <math> A + B</math> | ||
=Not Gates= | =Not Gates= | ||
| Line 35: | Line 39: | ||
[[File:NotGate.jpg|400px]] | [[File:NotGate.jpg|400px]] | ||
| + | ===Boolean Equation=== | ||
| + | <math> \overline{A}</math> | ||
=NAND Gate= | =NAND Gate= | ||
| Line 40: | Line 46: | ||
A NAND gate is an inverted AND gate meaning the inputs will cause an inverted outcome, so having no input will cause an output of 1, which is the opposite of an AND gate, which would be 0. | A NAND gate is an inverted AND gate meaning the inputs will cause an inverted outcome, so having no input will cause an output of 1, which is the opposite of an AND gate, which would be 0. | ||
| − | [[File:Nand Gate.png|200px]] [[File:Nand truth table.png|200px]] | + | [[File:Nand Gate.png|200px]] |
| + | |||
| + | ===Truth Table=== | ||
| + | [[File:Nand truth table.png|200px]] | ||
| + | |||
| + | ===Boolean Equation=== | ||
| + | <math> \overline{A \cdot B}</math> | ||
=NOR Gate= | =NOR Gate= | ||
| Line 48: | Line 60: | ||
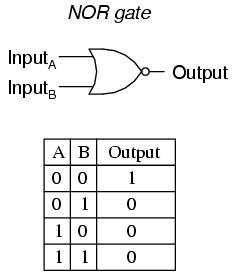
[[File:Nor gate and truth table.png]] | [[File:Nor gate and truth table.png]] | ||
| + | |||
| + | ===Boolean Equation=== | ||
| + | <math> \overline{ A + B }</math> | ||
=XOR Gate= | =XOR Gate= | ||
| Line 53: | Line 68: | ||
| − | [[File:XOR Gate.png|300px]] [[File:Truth table xor.png]] | + | [[File:XOR Gate.png|300px]] |
| + | |||
| + | ===Truth Table=== | ||
| + | [[File:Truth table xor.png]] | ||
| + | |||
| + | ===Boolean Equation=== | ||
| + | <math> A \oplus B</math> | ||
| + | |||
| + | or alternatively: | ||
| + | |||
| + | <math> \overline{A} \cdot B + A \cdot \overline{B}</math> | ||
Latest revision as of 09:32, 23 August 2023
Contents
[hide]And Gates
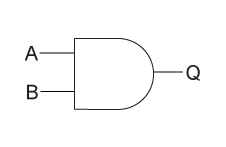
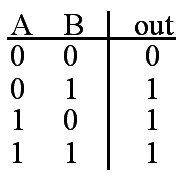
The output of an AND gate is true only when all of the inputs are true. If one or more of an AND gate's inputs are false, then the output of the AND gate is false.
Truth Table
| A | B | Out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Boolean Equation
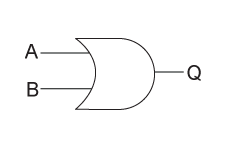
Or Gates
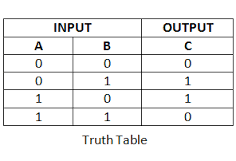
An OR gate is when either of the values can be true, and the output shall always be true in that instance. The images below shows what the OR gate looks like, and the table shows all possible outcomes.
Truth Table
Boolean Equation
Not Gates
A NOT gate outputs the opposite of what is inputted. The image below shows a NOT gate, as well as all possible outcomes.
Boolean Equation
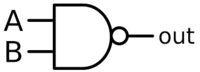
NAND Gate
A NAND gate is an inverted AND gate meaning the inputs will cause an inverted outcome, so having no input will cause an output of 1, which is the opposite of an AND gate, which would be 0.
Truth Table
Boolean Equation
NOR Gate
A NOR gate is an inverted OR gate, so any input will cause an output of 0 and this is the opposite of a regular OR gate, which would give an output of 1.
Boolean Equation
XOR Gate
An XOR gate is a variation of the OR gate, however, out of its two inputs, it will only give an output of 1 if only one of the inputs is 1, and an output of 0 if both are off or if both are on.
Truth Table
Boolean Equation
or alternatively: