Difference between revisions of "De Morgan's Law"
(→The Process) |
(→Video) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
https://www.youtube.com/watch?v=HoH0PrS3WNI&list=PLCiOXwirraUA9HyHoqOaGBU_k6nBRCb22&index=6 | https://www.youtube.com/watch?v=HoH0PrS3WNI&list=PLCiOXwirraUA9HyHoqOaGBU_k6nBRCb22&index=6 | ||
| − | ===TRC | + | ===TRC Video=== |
| − | + | <youtube>https://www.youtube.com/watch?v=O3w4yGY90SU</youtube> | |
| + | |||
| + | https://www.youtube.com/watch?v=O3w4yGY90SU | ||
==The Process== | ==The Process== | ||
| Line 50: | Line 52: | ||
1. Swap the sign: | 1. Swap the sign: | ||
| − | <math> \overline{(\overline{A | + | <math> \overline{(\overline{A+B})+\overline{A}} </math> |
| − | 2. Negate each | + | 2. Negate each term: |
| − | <math> \overline{(A | + | <math> \overline{\overline{\overline{(A+B)}}+\overline{\overline{A}}} </math> |
3. Negate the whole Expression: | 3. Negate the whole Expression: | ||
| − | <math>(A | + | <math> \overline{\overline{\overline{\overline{(A+B)}}+\overline{\overline{A}}}} </math> |
| + | |||
| + | Or: | ||
| + | |||
| + | <math>(A+B)+A </math> | ||
Using Redundancy law this expression can be simplified to: | Using Redundancy law this expression can be simplified to: | ||
Latest revision as of 09:05, 23 August 2023
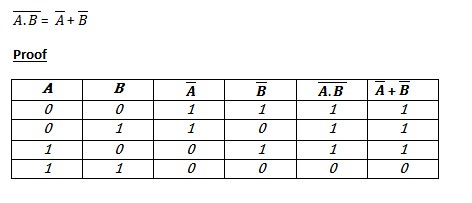
DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements. They can be easily remembered by "break the line, change the sign". The following image is how to prove De Morgan's Law...
Further explanation:
Video
https://www.youtube.com/watch?v=HoH0PrS3WNI&list=PLCiOXwirraUA9HyHoqOaGBU_k6nBRCb22&index=6
TRC Video
https://www.youtube.com/watch?v=O3w4yGY90SU
The Process
Step 1 - Reverse the sign
Step 2 - Negate each term
Step 3 - Negate the whole expression
It is recommended to "Break the longest line" when applying De Morgan's law.
You can often treat a whole set of brackets as a single term.
How to apply
Example 1
Now we use De Morgan's law to the whole equation and we treat A+B as one.
Example 2
Example 3
Simplifying by using De Morgan's Law:
1. Swap the sign:
2. Negate each term:
3. Negate the whole Expression:
Or:
Using Redundancy law this expression can be simplified to:
This is because if A is 1, the output will always be 1, regardless of the value of B.
Example 4
Applying De Morgan's law to the inner bracket
Inverting the not gate above the bracket
Swapping signs
Inverting not gates above terms
Applying De Morgan's law to the right bracket
Inverting the top not gate
Swapping signs
Inverting not gates above terms
Now that it is easier to simplify, we can do that
Applying the distributive law
Applying an identity law
Expand the brackets
Use identity
Use identity
Example 5
Example 6
Example 7