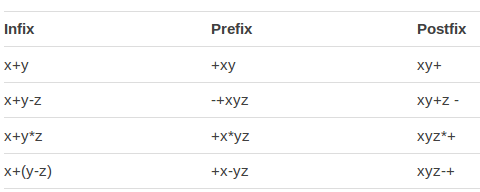Difference between revisions of "Reverse Polish"
(→Prefix - Infix - Postfix) |
(→Reverse Polish / Post fix Notation) |
||
| Line 4: | Line 4: | ||
Infix is standard maths notation, prefix is Polish Notation, and postfix is Reverse Polish Notation. You only need to know about Reverse Polish. | Infix is standard maths notation, prefix is Polish Notation, and postfix is Reverse Polish Notation. You only need to know about Reverse Polish. | ||
| − | ==Reverse Polish | + | ==Reverse Polish Notation== |
Reverse Polish Notation is a mathematical notation, in which the operator follows the operands. The result is the removal of the need for parenthesis, because each operation only applies to a fixed number of values. You start from left to right and move to the first operator, this applies to the 2 previous terms. | Reverse Polish Notation is a mathematical notation, in which the operator follows the operands. The result is the removal of the need for parenthesis, because each operation only applies to a fixed number of values. You start from left to right and move to the first operator, this applies to the 2 previous terms. | ||
Revision as of 21:34, 21 May 2017
Prefix - Infix - Postfix
Infix is standard maths notation, prefix is Polish Notation, and postfix is Reverse Polish Notation. You only need to know about Reverse Polish.
Reverse Polish Notation
Reverse Polish Notation is a mathematical notation, in which the operator follows the operands. The result is the removal of the need for parenthesis, because each operation only applies to a fixed number of values. You start from left to right and move to the first operator, this applies to the 2 previous terms.
You then move to the next operator to the right.
For example:
"3 4 +" is equal to 7, 3 + 4 using Infix notation.
"3 4 + 2 *" is equal to 14, (3+4)*2.
Because the operator applies to only two values (in this case) before it, there is no need for parenthesis.