Difference between revisions of "Turing Machines"
(→Transition functions) |
(→Transition functions) |
||
| Line 52: | Line 52: | ||
transition function (current state, input symbol) = (next state, output symbol, movement) | transition function (current state, input symbol) = (next state, output symbol, movement) | ||
| − | for example: | + | for example the above Turing Machine will be: |
| + | |||
| + | δ( 1 , 1 ) = ( 2 , 1 , → ) | ||
| + | δ( 2 , 1 ) = ( 2 , 1 , → ) | ||
| + | δ( 2 , ẜ ) = ( 3 , 1 , → ) | ||
| + | δ( 3 , ẜ ) = ( 4 , ẜ , ← ) | ||
| + | δ( 4 , 1 ) = ( 4 , 1 , ← ) | ||
| + | δ( 4 , ẜ ) = ( Stop , ẜ , → ) | ||
==Universal Turing Machine== | ==Universal Turing Machine== | ||
Revision as of 07:30, 22 May 2017
Contents
Definition
A Turing machine (TM) is a finite state machine that controls one or more tapes, where at least one tape is of unbounded length (i.e. infinitely long).
Explanation
A Turing machine describes an algorithm. A computer uses a computer program that is an implementation of an algorithm. Turing machines therefore can be used to make statements about an algorithm that are independent of the architecture of a particular machine.
An algorithm running on a particular machine will have had to make decisions about how to store values (e.g. the precision of how to store a real number). This does not happen on a Turing machine, meaning a Turing machine is a more general representation of the algorithm.
Six Components
A Turing Machine should include:
- An input alphabet
- A tape that goes on infinitely in one direction (to the right)
- An output alphabet (characters that can be printed onto the tape)
- A tape head that is used to read the contents of the tape one cell at a time
- A finite set of states, including one start (initial) state
- A program (set of instructions) that tells us which state to change to, which direction to move the tape head and which member of the output alphabet to place on the tape – based on the current state and the input received.
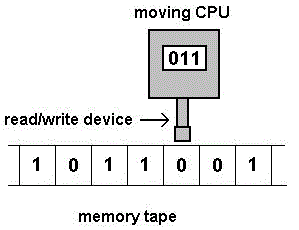
Tape / read write head
The read/write can move along the tape, any input comes from the current position of the tape and any output is written to the current position on the tape. Turing machines could have multiple tapes or even a two dimensional tape.
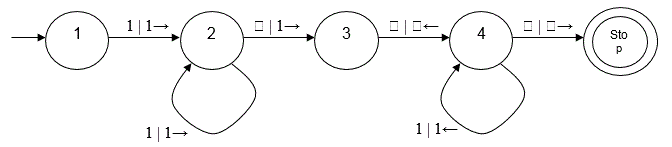
Example Machine
Each transition is labeled with the Input / Output. Movement of the Read Write Head is shown using arrows.
State transition table
| Original State | New State | Input | Output |
|---|---|---|---|
| 1 | 2 | 1 | 1→ |
| 2 | 2 | 1 | 1→ |
| 2 | 3 | ẜ | 1→ |
| 3 | 4 | ẜ | ẜ← |
| 4 | 4 | 1 | 1← |
| 4 | Stop | ẜ | ẜ→ |
Transition functions
The transition rules shown on the state transition diagram can also be represented in a state transition table or by using the state transition function δ (delta). This takes the form:
transition function (current state, input symbol) = (next state, output symbol, movement)
for example the above Turing Machine will be:
δ( 1 , 1 ) = ( 2 , 1 , → ) δ( 2 , 1 ) = ( 2 , 1 , → ) δ( 2 , ẜ ) = ( 3 , 1 , → ) δ( 3 , ẜ ) = ( 4 , ẜ , ← ) δ( 4 , 1 ) = ( 4 , 1 , ← ) δ( 4 , ẜ ) = ( Stop , ẜ , → )
Universal Turing Machine
Turing also realised that a Turing machine itself could be encoded and given as an input to another Turing machine. This universal Turing machine was capable of solving any problem that can be represented as an algorithm. A consequence of a universal Turing machine is that programs and data are really the same thing. A program is just a sequence of symbols that looks like any other piece of input but when fed to a universal machine this input wakes up and begins to compute. A computer downloads Java applets, e-mail viruses as data but can then proceed to execute them as programs.
A microprocessor is a universal machine. An embedded computer with a microprocessor at its core can be programmed to perform as a microcontroller by choosing the right set of program instructions. The program or programs are changed when a different functionality is required.
Principle of universality: a universal machine is a machine capable of simulating any other machine. A universal Turing machine, U, is an interpreter that reads the description of any arbitrary Turing machine and faithfully executes operations on data.
A task is computable if and only if it can be computed by a Turing machine.