Difference between revisions of "Shortest Path"

From TRCCompSci - AQA Computer Science
Jump to: navigation, search
(→‎Example)
Line 1: Line 1:
 
The shortest path is usually found by ''[https://www.youtube.com/watch?v=gdmfOwyQlcI Dijkstra's algorithm]''.  
 
The shortest path is usually found by ''[https://www.youtube.com/watch?v=gdmfOwyQlcI Dijkstra's algorithm]''.  
 
The algorithm functions as follows:
 
The algorithm functions as follows:
−
# The first node has a distance of 0, this is locked in and labeled node one.
+
 
−
# Each unlocked node that is connected directly to a locked node by a weighted arc is given a temporary label, equal to the total weight to reach it (from the starting node) if the new distance is less then any previously marked.
+
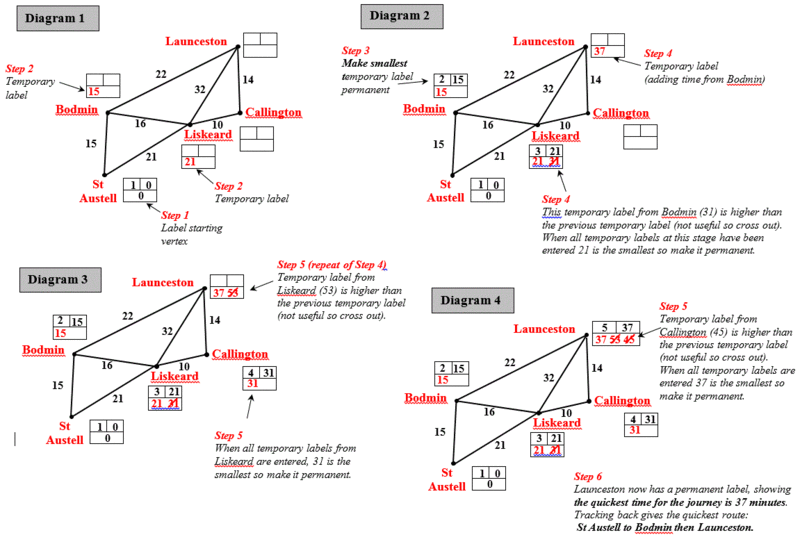
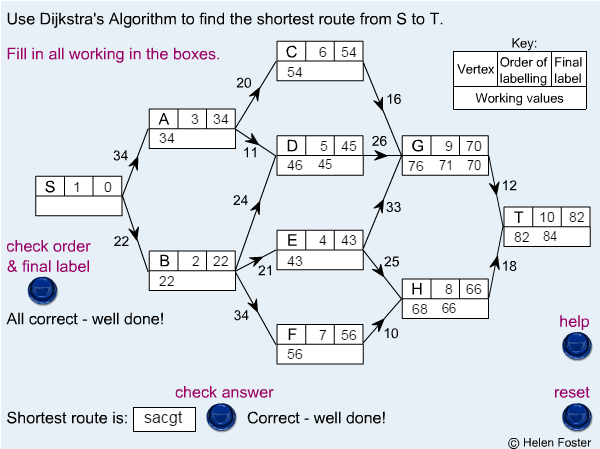
'''Step 1''' Give the permanent label 0 to the starting vertex.
−
# The node closest to the start is locked in with the shortest distance available and marked as the next node in the path.
+
 
−
# The previous 2 steps are repeated: the distance to the each unlocked node connected to a locked node is noted and the closest node to the start is selected (regardless of when the distance was given).
+
'''Step 2''' Give temporary labels to each vertex that is connected directly to the starting vertex.
−
# Once every node is marked, the shortest path would be the backwards path from the last node, where taking the arc reaches the distance on the locked in node until the final number is zero at the start.
+
 
−
#When every node is marked, the shortest path can be calculated by working backwards. From the shortest distance to the final node, subtract the weights of the connecting arcs. If the value is equal to shortest distance the connected node, it is part of the shortest path. It is possible for multiple shortest paths to exist.
+
'''Step 3''' Find the vertex with the smallest temporary label, number it and make it permanent.
 +
 
 +
'''Step 4''' Give temporary labels to each vertex that is connected directly to the previous vertex. Then find the vertex with the smallest temporary label, number it and make it permanent.
 +
 
 +
'''Step 5''' Repeat Step 4 until you have given a permanent label to the finishing vertex.
 +
 
 +
'''Step 6''' Use the permanent labels to trace back through the network to find the shortest path.
 +
 
 +
'''Step 7''' The shortest path is found by tracing back in such a way that an edge is only included if
 +
              its distance equals the change in label values.
 +
 
  
 
==Example==
 
==Example==

Revision as of 11:25, 23 May 2017

The shortest path is usually found by Dijkstra's algorithm. The algorithm functions as follows:

Step 1 Give the permanent label 0 to the starting vertex.

Step 2 Give temporary labels to each vertex that is connected directly to the starting vertex.

Step 3 Find the vertex with the smallest temporary label, number it and make it permanent.

Step 4 Give temporary labels to each vertex that is connected directly to the previous vertex. Then find the vertex with the smallest temporary label, number it and make it permanent.

Step 5 Repeat Step 4 until you have given a permanent label to the finishing vertex.

Step 6 Use the permanent labels to trace back through the network to find the shortest path.

Step 7 The shortest path is found by tracing back in such a way that an edge is only included if 

             its distance equals the change in label values.


Example

This is the starting graph and values:

Shortest path eg start.gif

The stages to identify the shortest path:

Shortest path example.gif

Further Example

Dijkstra.png

Retrieved from ‘http://www.trccompsci.online/mediawiki/index.php?title=Shortest_Path&oldid=2882’