Addition

Overview

Addition is covered from 0:00 until 5:46

https://www.youtube.com/watch?v=t15dhDG_WUA&list=PLCiOXwirraUDGCeSoEPSN-e2o9exXdOka&index=2 (0:00 - 5:46)

Alternatively, this is the PowerPoint to for this topic:

[1]

Binary Addition

Binary addition is being able to add two numbers together which are represented in binary form, which consist of 1s and 0s, you can add them together by converting them into denary, adding It together and then converting it back but its much faster to use the column addition method which you will see below.

There are four possibilities when adding binary numbers, these possibilities are:

a total of 0 (0+0) put down 0
a total of 1 (1+0, 0+1 or 0+0+carried 1) put down 1
a total of 2 (1+1) put down 0, carry 1
a total of 3 (1+1+ carried 1) put down 1, carry 1

For example, solve 6+7 using binary addition:

First convert 6 and 7 from denary to binary using your preferred method

6 = 4+2+0 = 110
7 = 4+2+1 = 111

Then add them keeping in mind the 4 possibilities and add each digit together, starting on the right:

110  +
111

So:

0+1 = 1

1+1 = 0 carry 1

1+1+ carried 1 = 1 carry 1

1 + 0 = 1

so 110+111 = 1101. Converting this number back to denary gives us an answer of 13.

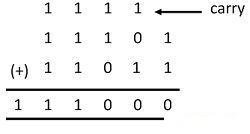
Another Example

Adding More Numbers Together

You could get 3 numbers to add however you wont be given a situation in which there are more than a total of 3.

For example:

101

101

011+

Which would = 1101

Adding Binary Numbers Into Denary

There are many ways to add two binary numbers together and get a denary value as the answer. The two main ways of doing are as follows: Method 1, Calculate the denary value of each binary number then add the two denary values together, you then should have the answer in denary. Or Method 2 which is just as simple. Add the two binary numbers together using 8-bit binary addition, then convert your binary answer into denary.

Example

01110100 + 00011111, Give your answer in denary.

Firstly, 01110100 can be converted into denary... 01110100 = 116.

Also, 00011111 when converted into denary is... 00011111 = 31.

116 + 31 = 147.

Another Example

01010110 + 11011001, Give your answer in denary.

Firstly, do 8-bit binary addition.

so:

01010110
        +
01011001

= 10101111

Then convert 10101111 into denary:

so:

10101111 = 175

Final Example

78 + 01010110, Give your answer in denary.

Since the question wants the answer in denary, we will firstly convert the binary value into denary so that we can properly add them together.

So:

01010110 = 86

Then we will add the two denary values together

78 + 86 = 164

If the question wanted the answer in 8-bit binary we would instead, convert the denary number into its binary value. And then we would add the two values together.

So:

     128 64 32 16 8 4 2 1
78 =  0   1  0  0 1 1 0 1
01001101
01001101 + 01010110 = 10100100
The answer is 10100100

Revision

1.

What is 00110101 + 01010001 in binary?

→ 1+1 = 2. Put down o, carry 1

→ 0+0+1 = 1. Put down 1, carry 0

→ 1+0 = 1. Put down 1, carry 0

→ 0+0 = 0. Put down 0 carry 0

→ 1+1 = 2. Put down 0, carry 1

→ 1+0+1 = 2. Put down 0, carry 1

→ 0+1+1 = 2. Put down 0, carry 1

→ 0+0+1 = 1. Put down 1, carry 0

→ 10000110

2.

What is 01110001 + 00011111 in denary?

→ 1+1 = 2. Put down 0, carry 1

→ 0+0+1 = 1. Put down 1, carry 0

→ 0+0 = 0. Put down 0, carry 0

→ 0+0 = 0.Put down 0, carry 0

→ 1+1 = 2. Put down 0, carry 1

→ 1+0+1 = 2. Put down 0, carry 1

→ 1+1+1 = 3. Put down 1, carry 1

→ 0+0+1 = 1. Put down 1, carry 0

→ 11000010

→ 128+64+2 = 194

3.

What is 01101110 + 01100101 in 8-bit binary?

→ 0 + 1 = 1. Put down 1, carry 0.

→ 1 + 0 = 1. Put down 1, carry 0.

→ 1 + 1 = 2. Put down 0, carry 1.

→ 0 + 1 + 1 = 2. Put down 0, carry 1.

→ 0 + 0 + 1 = 1. Put down 1, carry 0.

→ 1 + 1 = 2. Put down 0, carry 1.

→ 1 + 1 + 1 = 3. Put down 1, carry 1.

→ 0 + 0 + 1 = 1. Put down 1, carry 0.

→ 11010011

4.

What is it called when the numbers adds together to make a number bigger than 255 so doesn't fit into the 8 bits?

→ This is an overflow.

5. What do you do when you have an overflow?

	Add it anyway and then forget the overflow
	Add an extra bit
	give up
	Subtract the numbers instead

6.

What is 01100010 + 01001101 in 8 bit binary?

→ Add the one no carry

→ Add the one no carry

→ Add the one no carry

→ Add the one no carry

→ Don't add anything because its zero

→ Add the one no carry

→ Add the one carry the 1

→ Add the carry to the 0's so its a 1

7.

What is 10110100 + 00110101 in 8 bit binary?

8.

What is 11001100 + 10101010 in 8 bit binary?

9.

What is 11010101 + 01011100 in 8 bit binary?

10.

What is 10101111 + 01101101 in 8 bit binary?

11.

What is 10101100 + 01001100 in 8 bit binary?

12.

What is 11001010 + 01001111 in 8 bit binary?

13.

What is 011101 + 01000001 in 8 bit binary?

14.

What is 11111100 + 11000010 in 8 bit binary?

15.

What is 11010111 + 11100111 in 8 bit binary?

16.

What is 10110011 + 11001111 in 8 bit binary?

17.

What is 11111000 + 00011101 in 8 bit binary?

18.

What is 11000011 + 01101100 in 8 bit binary?

19.

What is 110010 + 11100111 in 8 bit binary?

20.

What is 11011010 + 11110010 in 8 bit binary?

Your score is 0 / 0