De Morgan's Law

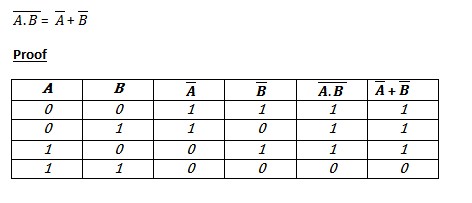
DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements. They can be easily remembered by "break the line, change the sign". The following image is how to prove De Morgan's Law...

Further explanation:

Video

https://www.youtube.com/watch?v=HoH0PrS3WNI&list=PLCiOXwirraUA9HyHoqOaGBU_k6nBRCb22&index=6

The Process

Step 3 - Negate the whole expression

It is recommended to "Break the longest line" when applying De Morgan's law.

You can often treat a whole set of brackets as a single term.

How to apply

Example 1

[math] \overline{(\overline{A+B})+B} [/math]

Now we use De Morgan's law to the whole equation and we treat A+B as one.

[math] (A+B).\overline {B} [/math]

[math] \overline {B}.A + (\overline{B}.B) [/math]

[math] \overline{B}.A + 0 [/math]

[math] \overline{B}.A [/math]

Example 2

[math](\overline{A+\overline{B}).\overline{A}}[/math]

Example 3

[math] \overline{(\overline{A+B}).\overline{A}} [/math]

Simplifying by using De Morgan's Law:

1. Swap the sign:

[math] \overline{(\overline{A+B})+\overline{A}} [/math]

2. Negate each term:

[math] \overline{\overline{\overline{(A+B)}}+\overline{\overline{A}}} [/math]

3. Negate the whole Expression:

[math] \overline{\overline{\overline{\overline{(A+B)}}+\overline{\overline{A}}}} [/math]

Or:

[math](A+B)+A [/math]

Using Redundancy law this expression can be simplified to:

[math] A [/math]

This is because if A is 1, the output will always be 1, regardless of the value of B.

Example 4

[math] (\overline{A} + B) . \overline{(A + (\overline{B + A})}) [/math]

Applying De Morgan's law to the inner bracket

[math] (\overline{A} + B) . \overline{(A + (B + A)}) [/math] Inverting the not gate above the bracket

[math] (\overline{A} + B) . \overline{(A + (B . A)}) [/math] Swapping signs

[math] (\overline{A} + B) . \overline{(A + (\overline{B} . \overline{A})}) [/math] Inverting not gates above terms

Applying De Morgan's law to the right bracket

[math] (\overline{A} + B) . (A + (\overline{B} . \overline{A})) [/math] Inverting the top not gate

[math] (\overline{A} + B) . (A . (\overline{B} + \overline{A})) [/math] Swapping signs

[math] (\overline{A} + B) . (\overline{A} . (B + A)) [/math] Inverting not gates above terms

Now that it is easier to simplify, we can do that

[math] (\overline{A} + B) . ((\overline{A} . B) + (\overline{A} . A))) [/math] Applying the distributive law

[math] (\overline{A} + B) . ((\overline{A} . B) + 0)) [/math] Applying an identity law

[math] (\overline{A} + B) . (\overline{A} . B) [/math]

[math] (\overline{A} . \overline{A} . B) + (B . \overline{A} . B) [/math] Expand the brackets

[math] (\overline{A} . B) + (\overline{A} . B) [/math] Use identity [math] X . X = X [/math]

[math] \overline{A} . B [/math] Use identity [math] X + X = X [/math]

Example 5

[math] \overline{\overline{(\overline{A}+A.(A+B))} + (B . C)} [/math]

Example 6

[math] \overline{\overline{(A+A.(\overline{A+B}))} + (B . C)} [/math]

Example 7

[math] \overline{(\overline{A}+A.(A+B))} + \overline{(B.C)} [/math]

[math] \overline{(\overline{A}+A+A.B)}+(\overline{B}+\overline{C}) [/math]

[math] (A.\overline{A}.\overline{A}+\overline{B})+(\overline{B}+\overline{C}) [/math]

[math] (A.\overline{A}+\overline{B})+(\overline{B}+\overline{C}) [/math]

[math] (0+\overline{B})+(\overline{B}+\overline{C}) [/math]

[math] \overline {B}+(\overline{B}+\overline{C}) [/math]

[math] \overline{C}+(\overline{B}+\overline{B}) [/math]

[math] \overline{B}+\overline{C} [/math]