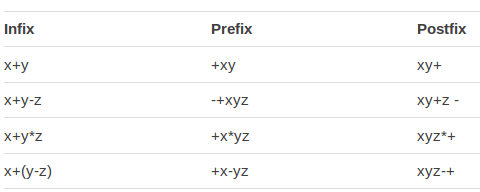Difference between revisions of "Reverse Polish"
| Line 1: | Line 1: | ||
| + | ==Prefix - Infix - Postfix== | ||
| + | [[File:notation.png]] | ||
| + | |||
| + | ==Reverse Polish / Post fix Notation== | ||
Reverse Polish Notation is a mathematical notation, in which the operator follows the operands. The result is the removal of the need for parenthesis, because each operation only applies to a fixed number of values. You start from left to right and move to the first operator, this applies to the 2 previous terms. | Reverse Polish Notation is a mathematical notation, in which the operator follows the operands. The result is the removal of the need for parenthesis, because each operation only applies to a fixed number of values. You start from left to right and move to the first operator, this applies to the 2 previous terms. | ||
Revision as of 21:30, 21 May 2017
Prefix - Infix - Postfix
Reverse Polish / Post fix Notation
Reverse Polish Notation is a mathematical notation, in which the operator follows the operands. The result is the removal of the need for parenthesis, because each operation only applies to a fixed number of values. You start from left to right and move to the first operator, this applies to the 2 previous terms.
You then move to the next operator to the right.
For example:
"3 4 +" is equal to 7, 3 + 4 using Infix notation.
"3 4 + 2 *" is equal to 14, (3+4)*2.
Because the operator applies to only two values (in this case) before it, there is no need for parenthesis.