Difference between revisions of "Tree Traversals"
(→Infix / Polish / Reverse Polish) |
(→Infix / Polish / Reverse Polish) |
||
| Line 37: | Line 37: | ||
==Infix / Polish / Reverse Polish== | ==Infix / Polish / Reverse Polish== | ||
If you create a binary tree for any given expression: | If you create a binary tree for any given expression: | ||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 49: | Line 48: | ||
| Post Order || Reverse Polish | | Post Order || Reverse Polish | ||
|} | |} | ||
| + | |||
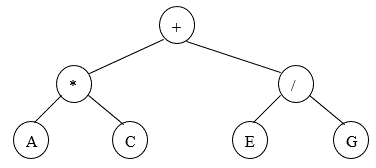
| + | For example: | ||
| + | |||
| + | [[File:ExpressionBinaryTree.gif]] | ||
| + | |||
| + | pre-order will give: | ||
| + | +*AC/EG | ||
| + | In-order will give: | ||
| + | A*C+E/G (order of evaluation is (A*C) + (E/G)) | ||
| + | Post-order will give: | ||
| + | AC*EG/+ (Reverse Polish form) | ||
Revision as of 07:56, 22 May 2017
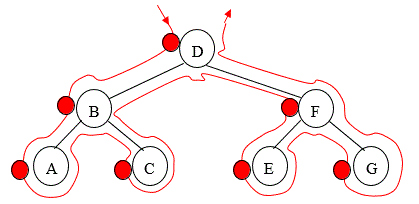
Pre Order
Starting to the left of the root, draw an outline around the tree as shown in Figure 10. As you pass to the left of a node (where the red dot is marked) output the data in that node, i.e. DBACFEG
Algorithm
- If tree empty do nothing
Otherwise
- Visit the root (e.g. print the value of the data item at the root)
- Traverse the left sub-tree in pre-order
- Traverse the right sub-tree in pre-order
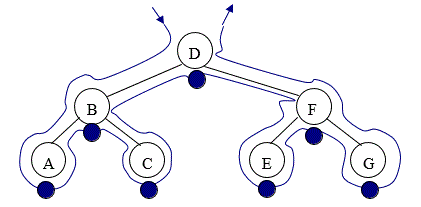
In Order
Starting to the left of the root, draw an outline around the tree as shown in Figure 11. As you pass underneath a node (where the blue dot is marked) output the data in that node, i.e. ABCDEFG
Algorithm:
- If tree empty do nothing
Otherwise:
- Traverse the left sub-tree in in-order
- Visit the root
- Traverse the right sub-tree in in-order
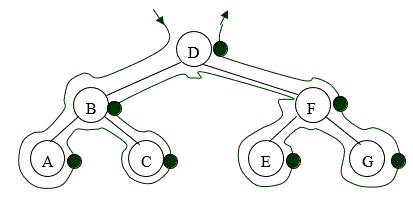
Post Order
Starting to the left of the root, draw an outline around the tree as shown in Figure 12. As you pass to the right of a node (where the green dot is marked) output the data in that node, i.e. ACBEGFD
Algorithm:
- If tree empty do nothing
Otherwise:
- Traverse the left sub-tree in post-order
- Traverse the right sub-tree in post-order
- Visit the root
Infix / Polish / Reverse Polish
If you create a binary tree for any given expression:
| Traversal | Notation |
|---|---|
| Pre Order | Polish |
| In Order | Infix |
| Post Order | Reverse Polish |
For example:
pre-order will give:
+*AC/EG
In-order will give:
A*C+E/G (order of evaluation is (A*C) + (E/G))
Post-order will give:
AC*EG/+ (Reverse Polish form)