Regular Expressions

A regular expression is a notation for defining all the valid strings of a formal language.

Examples of Regular Expression Notation

Regular Expression	Meaning
a	Matches a string consisting of just the symbol a
b	Matches a string consisting of just the symbol b
ab	Matches a string consisting of the symbol a followed by the symbol b
a*	Matches a string consisting of zero or more a’s
a+	Matches a string consisting of one or more a’s
abb?	Matches the string ab or the string abb. The ? symbol indicates zero or one of the preceding element
a|b	Matches a string consisting of the symbol a or the symbol b

Precedence Rules

When using regular expressions, the rules of arithmetic precedence are as follows:

+ and * are done first

Concatenation (ie joining elements together) is done next

| comes last

More Examples

Examples of regular expressions using the alphabet {a, b, c}

• abc defines the language with only the string ‘abc’
• abc | cba defines the language with two strings’ abc’ and ‘cba’
• (a | b) c (a | b) gives four strings: ‘aca’, ‘acb’, ‘bca’, ‘bcb’
• a+ gives an infinite number of strings: ‘a’, ‘aa’, ‘aaa’, etc
• ab* gives an infinite number of strings: ‘a’, ‘ab’, ‘abb’, ‘abbb’, etc
• (ab)* gives an infinite number of strings: ‘’, ‘ab’, ‘abab’, ‘ababab’, etc
• (a | c)+ gives all possible strings of a and c (not including the empty string)

Regular expression meta-characters

Symbol	Meaning	Example
│	Used to separate alternatives	a│b (Means a or b)
?	Used to denote zero or one of the preceding element	a? (0 or 1 as; matches with ‘’ & ‘a’)
*	Used to denote zero or more of the preceding element	a* (0 or more as; matches with ‘’, ‘a’, ‘aa’, etc.)
+	Used to denote one or more of the preceding element	a+ (1 or more as; matches with ‘a’, ‘aa”’etc.)
( )	Used to group characters together, to indicate the scope of another operator	(ab)* (Example 0 or more abs; matches with ‘’, ‘ab’, ‘abab’, etc.
[ ]	Another way of denoting alternatives (instead of vertical bar). Defines a character class	[ab] (means a or b)
\	The escape character (this turns the metacharacter into an ordinary character)	a\* (the a character followed by the * character. Note: \ is needed as a* would mean zero or more as.)
^	Used to indicate the negation of a character class. Also used to match the position before the first character in a string	a[^bc] (a followed by a character that is not a b or c) ^abc will match with abc only if it is at the beginning of a string
$	Used to match with the position after the last character in a string	abc$ (will match with abc only if it is at the end of a string)
.	Matches with any single character	a.a (will match with any string that has an a followed by any character followed by an a e.g. ‘aca’, ‘aba’)
-	Used to specify a range of values in a character class	[A-Z] (character in the range of A to Z)

Regular Language

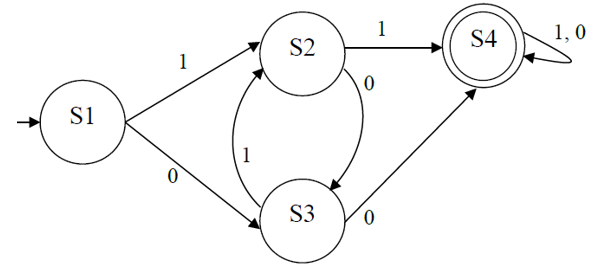
A regular language is a formal language that can be accepted by a finite state machine. Regular Expressions can also be specified using a FSM, an example question:

The FSM in below defines the language that allows all strings containing at least, either two consecutive 1s or two consecutive 0s.
The strings 0110, 00 and 01011 are all accepted by the FSM and so are valid strings in the language.
The strings 1010 and 01 are not accepted by the FSM and so are not valid strings in the language.

For 3 marks you need to write the regular expression that matches this FSM.