Difference between revisions of "Shortest Path"
(→Example) |
(→Example) |
||
| Line 22: | Line 22: | ||
[[File:Shortest path eg start.gif|600px]] | [[File:Shortest path eg start.gif|600px]] | ||
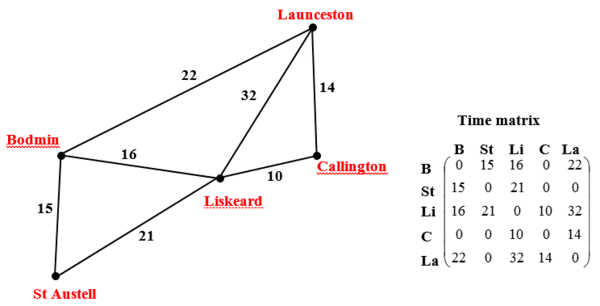
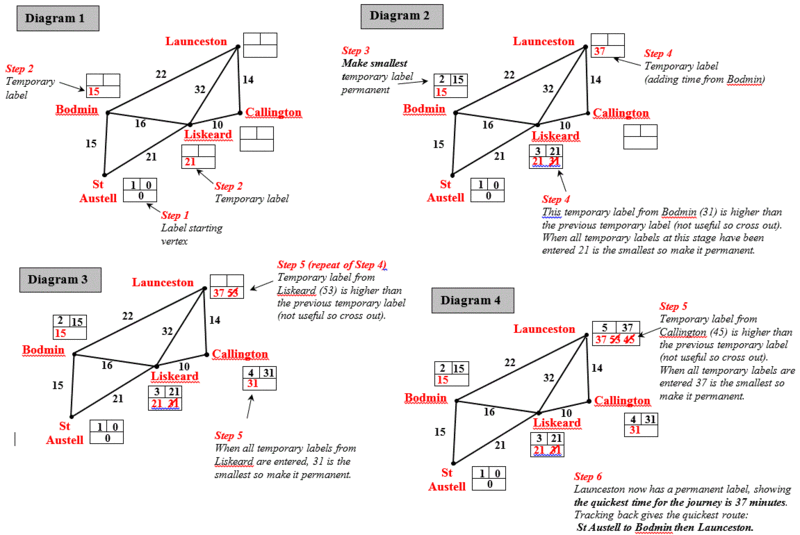
| − | The stages to identify the shortest path: | + | The stages to identify the shortest path from '''St. Austell''' to '''Launceston''': |
[[File:Shortest path example.gif|800px]] | [[File:Shortest path example.gif|800px]] | ||
Revision as of 12:28, 23 May 2017
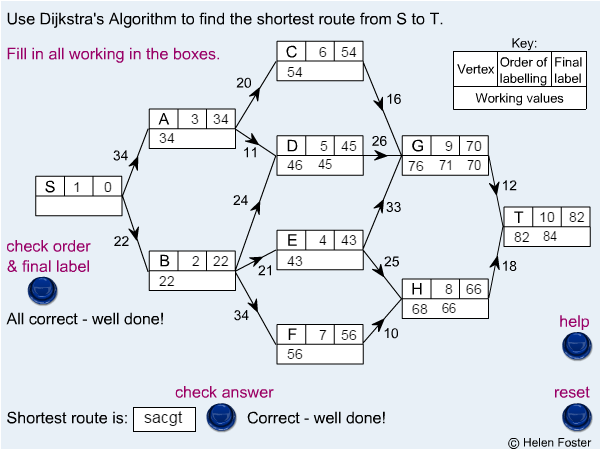
The shortest path is usually found by Dijkstra's algorithm. The algorithm functions as follows:
Step 1 Give the permanent label 0 to the starting vertex.
Step 2 Give temporary labels to each vertex that is connected directly to the starting vertex.
Step 3 Find the vertex with the smallest temporary label, number it and make it permanent.
Step 4 Give temporary labels to each vertex that is connected directly to the previous vertex. Then find the vertex with the smallest temporary label, number it and make it permanent.
Step 5 Repeat Step 4 until you have given a permanent label to the finishing vertex.
Step 6 Use the permanent labels to trace back through the network to find the shortest path.
Step 7 The shortest path is found by tracing back in such a way that an edge is only included if its distance equals the change in label values.
Example
This is the starting graph and values:
The stages to identify the shortest path from St. Austell to Launceston: