Difference between revisions of "Number Systems / Number Bases"
(→Denary Number system) |
(→Denary Number system) |
||
| Line 7: | Line 7: | ||
This means the number 10 in denary would be 1 ‘ten’ plus 0 ‘units’ | This means the number 10 in denary would be 1 ‘ten’ plus 0 ‘units’ | ||
The first column, the one on the far right, s 10 to the power 0. For each subsequent column the power is increased by 1. | The first column, the one on the far right, s 10 to the power 0. For each subsequent column the power is increased by 1. | ||
| − | [[File: | + | [[File:a68ec88b918976a97c85a9df1a08b912.jpg]] |
=Binary Number System= | =Binary Number System= | ||
Revision as of 14:56, 14 December 2016
Number Systems
The number systems used in Computer Science are often referred to as Base 16, Base 10, Base 8, or Base 2. The number base specifies how many digits are used (Including Zero) and how much each digit is multiplied by as it is moved from right to left.
Denary Number system
Also sometimes referred to as the Decimal number system, the Denary number system uses the digits 0-9 which means there are 10 possible digits.
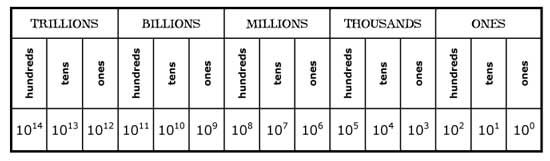
If we go beyond the digit 9 in denary another column is used; i.e the ‘tens’ column or the ‘Hundreds’ Column.
This means the number 10 in denary would be 1 ‘ten’ plus 0 ‘units’
The first column, the one on the far right, s 10 to the power 0. For each subsequent column the power is increased by 1.