Difference between revisions of "Graphs"
Mfrederick (talk | contribs) (→Comparison of List VS Matrix) |
m (Moved the list picture into the list and the matrix picture into the matrix section) |
||
| Line 24: | Line 24: | ||
==Adjacency Matrix== | ==Adjacency Matrix== | ||
| − | [[File:Graph- | + | [[File:Graph-3.jpg|thumb|300px]] |
An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other. | An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other. | ||
<br /> | <br /> | ||
| Line 35: | Line 35: | ||
==Adjacency List== | ==Adjacency List== | ||
| − | [[File:Graph- | + | [[File:Graph-2.jpg|thumb|300px]] |
This is a list shown in binary for the values that are going to be connected. It usually helps to transfer the matrices into a list first before you turn it into a graph to make things easier. | This is a list shown in binary for the values that are going to be connected. It usually helps to transfer the matrices into a list first before you turn it into a graph to make things easier. | ||
<br /> | <br /> | ||
Revision as of 20:49, 6 December 2017
Contents
[hide]What is a graph
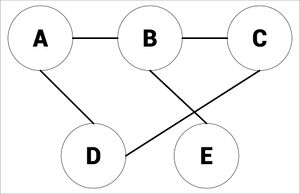
A graph is an abstract data structure. It can be used to solve routine problems.
Vertices connected by an edge (see picture) are called Neighbours.
The degree of a vertex is how many things are connected to it, in the picture, there would be 2.
Edges can also be called connectors and vertex can also be called nodes or entries.
Terms
weighted graph
Each edge/arc has an associated value, which can be used for distance, cost and so on.
vertex/node
An entity, location within the graph (represented by a circle).
edge/arc
A connection between two vertex/nodes
undirected graph
You can travel either direction on an edge/arc. For example an edge between A & B allows movement from A to B and from B to A.
directed graph
Each edge/arc will have an arrow to indicate the direction of travel. This will require additional edges to cover both directions.
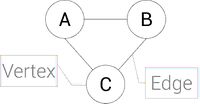
Adjacency Matrix
An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other.
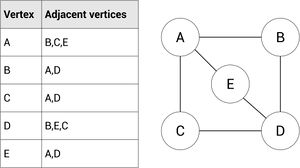
Adjacency List
This is a list shown in binary for the values that are going to be connected. It usually helps to transfer the matrices into a list first before you turn it into a graph to make things easier.
Comparison of List VS Matrix
| List | Matrix |
|---|---|
| Its quicker to find an edge | Needs to look at all items |
| Less space, no wastage | Stores information about each edge |