Difference between revisions of "Tree Traversals"
(→Infix / Polish / Reverse Polish) |
|||
| Line 1: | Line 1: | ||
| + | ==Overview== | ||
| + | <youtube>https://www.youtube.com/watch?v=4Tg0Fg6qzJY&index=2&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=4Tg0Fg6qzJY&index=2&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E | ||
| + | |||
==Pre Order== | ==Pre Order== | ||
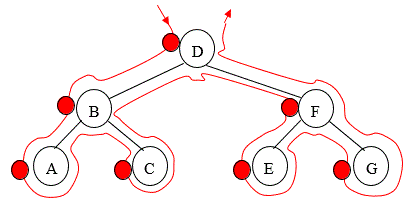
Starting to the left of the root, draw an outline around the tree as shown in Figure 10. As you pass to the left of a node (where the red dot is marked) output the data in that node, i.e. DBACFEG | Starting to the left of the root, draw an outline around the tree as shown in Figure 10. As you pass to the left of a node (where the red dot is marked) output the data in that node, i.e. DBACFEG | ||
Latest revision as of 12:36, 11 June 2018
Overview
https://www.youtube.com/watch?v=4Tg0Fg6qzJY&index=2&list=PLCiOXwirraUB0HOYmEbmx-7KStKtoXZ6E
Pre Order
Starting to the left of the root, draw an outline around the tree as shown in Figure 10. As you pass to the left of a node (where the red dot is marked) output the data in that node, i.e. DBACFEG
Algorithm
- If tree empty do nothing
Otherwise
- Visit the root (e.g. print the value of the data item at the root)
- Traverse the left sub-tree in pre-order
- Traverse the right sub-tree in pre-order
In Order
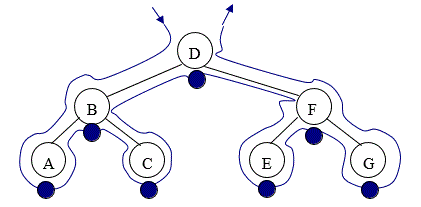
Starting to the left of the root, draw an outline around the tree as shown in Figure 11. As you pass underneath a node (where the blue dot is marked) output the data in that node, i.e. ABCDEFG
Algorithm:
- If tree empty do nothing
Otherwise:
- Traverse the left sub-tree in in-order
- Visit the root
- Traverse the right sub-tree in in-order
Post Order
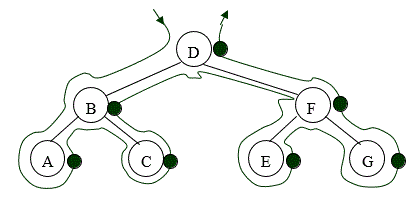
Starting to the left of the root, draw an outline around the tree as shown in Figure 12. As you pass to the right of a node (where the green dot is marked) output the data in that node, i.e. ACBEGFD
Algorithm:
- If tree empty do nothing
Otherwise:
- Traverse the left sub-tree in post-order
- Traverse the right sub-tree in post-order
- Visit the root
Infix / Polish / Reverse Polish
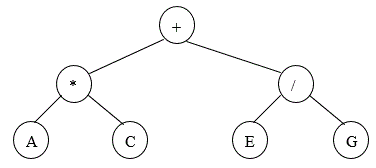
If you create a binary tree for any given expression:
| Traversal | Notation |
|---|---|
| Pre Order | Polish |
| In Order | Infix |
| Post Order | Reverse Polish |
For example:
pre-order will give:
+*AC/EG
In-order will give:
A*C+E/G (order of evaluation is (A*C) + (E/G))
Post-order will give:
AC*EG/+ (Reverse Polish form)