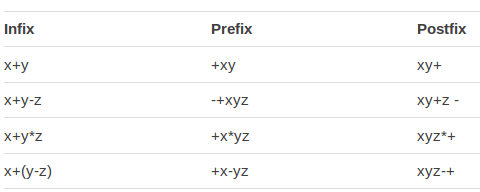Reverse Polish

Prefix - Infix - Postfix

Infix is standard maths notation, prefix is Polish Notation, and postfix is Reverse Polish Notation. You only need to know about Reverse Polish.

Reverse Polish Notation

Reverse Polish Notation is a mathematical notation, in which the operator follows the operands. The result is the removal of the need for parenthesis, because each operation only applies to a fixed number of values. You start from left to right and move to the first operator, this applies to the 2 previous terms. You then move to the next operator to the right.

For example:

"3 4 +" is equal to 7, 3 + 4 using Infix notation.

"3 4 + 2 *" is equal to 14, (3+4)*2.

Because the operator applies to only two values (in this case) before it, there is no need for parenthesis.

Process to reverse polish

All of the terms / values will stay in the same order, these should never be swap around.

Only the operators move, and for reverse polish the operators will move to the right of the values it operates on:

3 + 4 using Infix notation, become "3 4 +". The + is moved to the right and is after the values it operates on.

(3+4)*2 using infix notation becomes "3 4 + 2 *". The + has moved to the right and is after the values it operate on. The * has also moved to the right and again is now after the values it operates on.

Process from reverse polish

Moving from left to right find the first operator. This operator applies to the two previous values (so do this calculation, store the answer). From left to right move to the next operator, this operates on the 2 previous values (this could be the answer from a previous operator) Keep doing the calculation as you go, and when you have used every operator you should have your answer.

Remember the order of the values will never change, so 34+ is 3+4 and is never 4+3