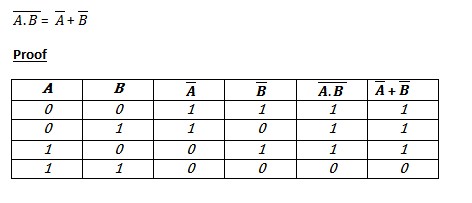
DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements. They can be easily remembered by "break the line, change the sign". The following image is how to prove De Morgan's Law...
The Process
Step 1 - Reverse the sign
Step 2 - Negate each term
Step 3 - Negate the whole expression
How to apply
Example 1
[math] \overline{(\overline{A+B})+B} [/math]
Example 2
[math](\overline{A+\overline{B}).\overline{A}}[/math]
Example 3
[math] \overline{((\overline{A+B}).\overline{A}} [/math]
Simplifying by using De Morgan's Law:
1. Swap the sign:
[math] \overline{((\overline{A.B})+\overline{A}} [/math]
2. Negate each expression:
[math] \overline{((A.B)+A} [/math]
3. Negate the whole Expression:
[math]((A.B)+A [/math]
Using Redundancy law this expression can be simplified to:
[math] A [/math]
This is because if A is 1, the output will always be 1, regardless of the value of B.
Example 4
[math] (\overline{A} + B) . \overline{(A + (\overline{B +A})}) [/math]
Example 5
[math] \overline{\overline{(\overline{A}+A.(A+B))} + (B . C)} [/math]
Example 6
[math] \overline{\overline{(A+A.(\overline{A+B}))} + (B . C)} [/math]
Example 7
[math] \overline{(\overline{A}+A.(A+B))} + \overline{(B.C)} [/math]
[math] \overline{(\overline{A}+A+A.B)}+(\overline{B}+\overline{C}) [/math]
[math] (A.\overline{A}.\overline{A}+\overline{B})+(\overline{B}+\overline{C}) [/math]
[math] (A.\overline{A}+\overline{B})+(\overline{B}+\overline{C}) [/math]
[math] (0+\overline{B})+(\overline{B}+\overline{C}) [/math]
[math] \overline {B}+(\overline{B}+\overline{C}) [/math]
[math] \overline{C}+(\overline{B}+\overline{B}) [/math]
[math] \overline{B}+\overline{C} [/math]
